
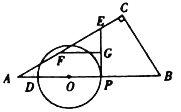
【题目】如图,AB、AC分别是⊙O的直径和弦,点D为劣弧AC上一点,弦DE⊥AB分别交⊙O于E,交AB于H,交AC于F.P是ED延长线上一点且PC=PF.
(1) 求证:PC是⊙O的切线;
(2) 点D在劣弧AC什么位置时,才能使![]() ,为什么?
,为什么?
(3) 在(2)的条件下,若OH=1,AH=2,求弦AC的长.

【答案】(1)证明见解析;(2)点D在劣弧AC中点位置时,才能使![]() ,理由见解析;(3)4
,理由见解析;(3)4![]() .
.
【解析】
(1)连结OC,证明∠OCP=90°即可;
(2)乘积的形式可以转化为比例的形式,通过证明三角形相似得出;
(3)可以先根据勾股定理得出DH,再通过证明△OGA≌△OHD,得出AC=2AG=2DH,求出弦AC的长.
(1)证明:连结OC
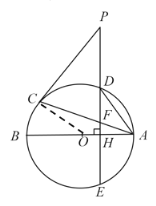
∵PC=PF,OA=OC
∴∠PCA=∠PFC,∠OCA=∠OAC
∵∠PFC=∠AFH,DE⊥AB
∴∠AHF=90°
∴∠PCO=∠PCA+∠ACO=∠AFH+∠FAH=90°
∴PC是⊙O的切线.
(2)解:点D在劣弧AC中点位置时,才能使![]() ,理由如下:
,理由如下:
连结AE
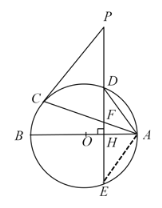
∵点D在劣弧AC中点位置
∴∠DAF=∠DEA
∵∠ADE=∠ADE
∴△DAF∽△DEA
∴AD∶DE=DF∶AD
∴![]()
(3)解:连结OD交AC于G
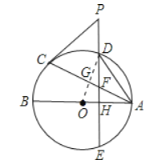
∵OH=1,AH=2
∴OA=3
即OD=3
∴DH=![]()
∵点D在劣弧AC中点位置
∴AC⊥DO
∴∠OGA=∠OHD=90°
在△OGA和△OHD中,
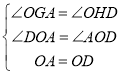
∴△OGA≌△OHD(AAS)
∴AG=DH
∴AC=4![]() .
.


科目:初中数学 来源: 题型:
【题目】某市中招体育测试改革,其中篮球和足球作为选考项目,某商店抓住这一商机决定购进一批篮球和足球共200个,这两种球的进价和售价如下表所示:
篮球 | 足球 | |
进价(元/个) | 180 | 150 |
售价(元/个) | 250 | 200 |
(1)若商店计划销售完这批球后能获利11600元,问篮球和足球应分别购进多少个?
(2)设购进篮球![]() 个,获利为
个,获利为![]() 元,求
元,求![]() 与
与![]() 之间的函数关系;
之间的函数关系;
(3)若商店计划投入资金不多于31560元且销售完这批球后商店获利不少于11000元,请问有哪几种购球方案,并写出获利最大的购球方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学兴趣小组想利用所学的知识了解某广告牌的高度,已知CD=2m.经测量,得到其它数据如图所示.其中∠CAH=37°,∠DBH=67°,AB=10m,请你根据以上数据计算GH的长.(参考数据![]() ,
,![]() ,
,![]() )
)
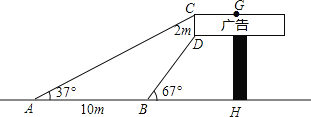
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=x+4的图象与反比例函数y=![]() (k为常数且k≠0)的图象交于A(﹣1,a),B两点,与x轴交于点C.
(k为常数且k≠0)的图象交于A(﹣1,a),B两点,与x轴交于点C.
(1)求此反比例函数的表达式;
(2)若点P在x轴上,且S△ACP=![]() S△BOC,求点P的坐标.
S△BOC,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】配餐公司为某学校提供A、B、C三类午餐供师生选择,三类午餐每份的价格分别是:A餐5元,B餐6元,C餐8元.为做好下阶段的营销工作,配餐公司根据该校上周A、B、C三类午餐购买情况,将所得的数据处理后,制成统计表(如下左图);根据以往销售量与平均每份利润之间的关系,制成统计图(如下右图).
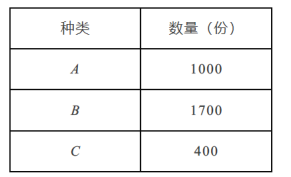
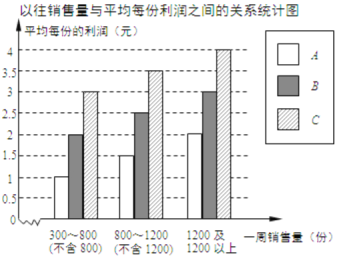
请根据以上信息,解答下列问题:
(1)该校师生上周购买午餐费用的众数是 元;
(2)配餐公司上周在该校销售B餐每份的利润大约是 元;
(3)请你计算配餐公司上周在该校销售午餐约盈利多少元.
查看答案和解析>>
科目:初中数学 来源: 题型:
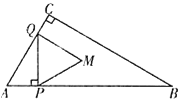
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 从点
从点![]() 出发以每秒2个单位的速度沿
出发以每秒2个单位的速度沿![]() 向终点
向终点![]() 运动,过点
运动,过点![]() 作
作![]() 的垂线交折线
的垂线交折线![]() 于点
于点![]() ,当点
,当点![]() 不和
不和![]() 的顶点重合时,以
的顶点重合时,以![]() 为边作等边三角形
为边作等边三角形![]() ,使点
,使点![]() 和点
和点![]() 在直线
在直线![]() 的同侧,设点
的同侧,设点![]() 的运动时间为
的运动时间为![]() (秒).
(秒).
(1)求等边三角形![]() 的边长(用含
的边长(用含![]() 的代数式表示);
的代数式表示);
(2)当点![]() 落在
落在![]() 的边
的边![]() 上时,求
上时,求![]() 的值;
的值;
(3)设![]() 与
与![]() 重合部分图形的面积为
重合部分图形的面积为![]() ,求
,求![]() 与
与![]() 的函数关系式;
的函数关系式;
(4)作直线![]() ,设点
,设点![]() 关于直线
关于直线![]() 的对称点分别为
的对称点分别为![]() ,直接写出
,直接写出![]() 时
时![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】郴州市正在创建“全国文明城市”,某校拟举办“创文知识”抢答赛,欲购买A、B两种奖品以鼓励抢答者.如果购买A种20件,B种15件,共需380元;如果购买A种15件,B种10件,共需280元.
(1)A、B两种奖品每件各多少元?
(2)现要购买A、B两种奖品共100件,总费用不超过900元,那么A种奖品最多购买多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
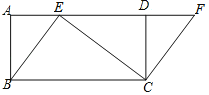
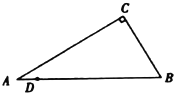
【题目】如图,四边形ABCD是矩形,点E在AD边上,点F在AD的延长线上,且BE=CF.
(1)求证:四边形EBCF是平行四边形.
(2)若∠BEC=90°,∠ABE=30°,AB=![]() ,求ED的长.
,求ED的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
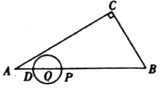
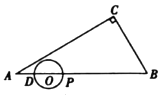
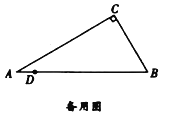
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 在线段
在线段![]() 上,
上,![]() .点
.点![]() 从
从![]() 点出发,沿
点出发,沿![]() 方向运动,以
方向运动,以![]() 为直径作
为直径作![]() ,当
,当![]() 运动到点
运动到点![]() 时停止运动,设
时停止运动,设![]() .
.
(1)![]() ___________,
___________,![]() ___________.(用
___________.(用![]() 的代数式表示)
的代数式表示)
(2)当![]() 为何值时,
为何值时,![]() 与
与![]() 的一边相切?
的一边相切?
(3)在点![]() 整个运动过程中,过点
整个运动过程中,过点![]() 作
作![]() 的切线交折线
的切线交折线![]() 于点
于点![]() ,将线段
,将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到
得到![]() ,过
,过![]() 作
作![]() 于
于![]() .
.

①当线段![]() 长度达到最大时,求
长度达到最大时,求![]() 的值;
的值;
②直接写出点![]() 所经过的路径长是________.(结果保留根号)
所经过的路径长是________.(结果保留根号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com