

分析 (1)根据l⊥ON,可得∠DBA+∠ABO=90°.由∠MON=90°,得∠ABO+∠BAO=90°,∠BAO=∠DBA.由题意知:∠BAD=90°,可得△ABO∽△BDA,从而求出OA
(2)分情况0≤t<1; 1≤t<4时; 4≤t≤5时,求出函数关系式.
(3)存在满足条件的t(0≤t≤4),分两种情况讨论①当PA′=PD时,PA′2=PD2,②当PA′=A′D时,PA′2=A′D2,讨论即可得出结论.
解答 解:(1)∵l⊥ON,
∴∠DBA+∠ABO=90°.
∵∠MON=90°,
∴∠ABO+∠BAO=90°,
∴∠BAO=∠DBA.
由题意知:∠BAD=90°,
∴∠BAD=∠AOB=90°,
∴△ABO∽△BDA.
∴$\frac{OB}{AD}=\frac{OA}{AB}$.
由题意知:AB=2AD,OB=4,
∴$\frac{4}{AD}=\frac{OA}{2AD}$,
∴OA=8.
(2)当0≤t<1时,如图1,
AA1=2t,OB=4,OA=8,AB=4$\sqrt{5}$,
∵△AFA1∽△AOB,
∴$\frac{OB}{AF}=\frac{{A}_{1}F}{OA}=\frac{A{A}_{1}}{AB}$,
∴AF=$\frac{4t}{\sqrt{5}}$,A1'F=$\frac{2t}{\sqrt{5}}$,
S=S△AFA1=$\frac{1}{2}$AF×A1F=$\frac{4}{5}{t}^{2}$.
当1≤t<4时,如图2,
在Rt△EHA2中,A2E=2t-2.A2A=2t.AE=2,
∵△EHA2∽△AOB,
∴$\frac{OB}{HE}=\frac{{A}_{2}E}{OA}$,
∴$\frac{4}{HE}=\frac{8}{2t-2}$
∴HE=t-1
∵△AGA2∽△AOB,
$\frac{AG}{OB}=\frac{{A}_{2}G}{OA}=\frac{A{A}_{2}}{AB}$,
∴$\frac{AG}{4}=\frac{{A}_{2}G}{8}=\frac{2t}{4\sqrt{5}}$,
∴AG=$\frac{2t}{\sqrt{5}}$,A2G=$\frac{4t}{\sqrt{5}}$,
∴S=$\frac{1}{2}$AG×A2N-$\frac{1}{2}$A2E×EH=-$\frac{1}{5}{t}^{2}-2t-1$.
当4≤t≤5时,如图3,
AA3=2t,OA=8,AE=2,OE=BD=10,AO3=2t-8,A3E=2t-2,
HE=t-1,HA3=$\sqrt{5}$(t-1),HD=5-t,
∵△DHG∽△HEA3,
∴$\frac{DH}{HE}=\frac{DG}{AH}=\frac{HG}{E{A}_{3}}$
∴HG=$\frac{5-t}{\sqrt{5}}$,DG=$\frac{2(5-t)}{\sqrt{5}}$,
∵△A3EH∽△AFO3,
∴$\frac{AH}{A{O}_{3}}=\frac{EH}{F{O}_{3}}=\frac{{A}_{3}E}{AF}$
∴FO3=4(4-t),
∴S=$\frac{1}{2}$AE×DE-$\frac{1}{2}$HE×A3E-$\frac{1}{2}$AO3×FO3=-$\frac{21}{5}{t}^{2}+34t-65$.
(3)存在满足条件的t(0≤t≤4),理由如下:
如图4,
由题意知:BB'=AA'=2t,O′A′=OA=8,DE=B′O′=BO=4.
∵△BB'P∽△AOB,
∴$\frac{BB'}{AO}=\frac{B'P}{BO}$,
即 $\frac{2t}{8}=\frac{B'P}{4}$,
∴B'P=t.
∵△DAE∽△ABO,
∴$\frac{AE}{BO}=\frac{DE}{AO}$,
即$\frac{AE}{4}=\frac{4}{8}$,
∴AE=2,
∴BD=OE=OA+AE=10.
∴PO′=4-t,B′D=10-2t,A′E=10-8-2t或2t+8-10.
在Rt△PO'A'中,PA'2=PO'2+O'A'2=t2-8t+80.
在Rt△PB'D中,PD2=PB'2+B'D2=5t2-40t+100.
在Rt△A'DE中,A'D2=DE2+A'E2=4t2-8t+20.
①当PA′=PD时,PA′2=PD2,即t2-8t+80=5t2-40t+100,
解得${t}_{1}=4+\sqrt{11}$.${t}_{2}=4-\sqrt{11}$
∵0≤t≤4,
∴t=4-$\sqrt{11}$.
②当PA′=A′D时,PA′2=A′D2,即t2-8t+80=4t2-8t+20,
解得t=±2$\sqrt{5}$.
∵0≤t≤4,
∴此种情况不成立.
③当PD=A'D时,PD2=A'D2,即:5t2-40t+100=4t2-8t+20,
∴t=16±4$\sqrt{11}$,
∵0≤t≤4,
∴t=16-4$\sqrt{11}$.
点评 此题是几何变换综合题,主要考查了平移的性质,相似三角形的判定和性质,勾股定理,直角三角形的性质,解本题的关键是画出图形,难点分类讨论.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小颖利用计算机画出了函数y=x3-3x2-x+4的图象(如图),根据图象,你能求得方程x3-3x2-x+4=0的近似根吗?请写出你的结果,并说出你的理由(结果保留小数点后一位)
小颖利用计算机画出了函数y=x3-3x2-x+4的图象(如图),根据图象,你能求得方程x3-3x2-x+4=0的近似根吗?请写出你的结果,并说出你的理由(结果保留小数点后一位)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
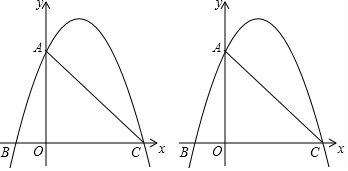
 如图,已知二次函数y=ax2+bx+c(a,b,c是常数,且a>0)的图象经过点A(3,6),并与x轴相交于B、C两点(点B在点C右侧),且S△ABC=12,∠ACB=45°.
如图,已知二次函数y=ax2+bx+c(a,b,c是常数,且a>0)的图象经过点A(3,6),并与x轴相交于B、C两点(点B在点C右侧),且S△ABC=12,∠ACB=45°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com