
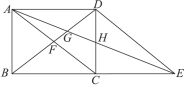
【题目】如图,在矩形ABCD中对角线AC,BD相交于点F,延长BC到点E,使得四边形ACED是一个平行四边形,平行四边形对角线AE交BD,CD分别为点G和点H.
(1)证明:DG2=FG·BG;
(2)若AB=5,BC=6,则线段GH的长度.
【答案】(2)见解析(2)![]()
【解析】
(1)由已知可证得△ADG∽△EBG,△AGF∽△EGD,根据相似三角形的对应边成比例即可得到DG2=FG·BG;
(2)由已知可得到DH,AH的长,又因为△ADG∽△EBG,从而求得AG的长,则根据GH=AHAG就得到了线段GH的长度.
解:(1)证明:∵ABCD是矩形,且AD∥BC,
∴△ADG∽△EBG.
∴![]() .
.
又∵△AGF∽△EGD,
∴![]() .
.
∴![]() .
.
∴DG2=FG·BG.
(2)∵ACED为平行四边形,AE,CD相交于点H,
∴DH=![]() DC=
DC=![]() AB=
AB=![]() ,AE=13.
,AE=13.
∴在直角三角形ADH中,![]()
∴AH=![]()
又∵△ADG∽△EBG,
∴![]() .
.
∴AG=![]() GE=
GE=![]() ×AE=
×AE=![]() ×13=
×13=![]() .
.
∴GH=AHAG=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,![]() 为
为![]() 直径,
直径,![]() 是
是![]() 上一点,
上一点,![]() 于点
于点![]() ,弦
,弦![]() 与
与![]() 交于点
交于点![]() .过点
.过点![]() 作
作![]() 的切线交
的切线交![]() 的延长线于点
的延长线于点![]() ,过点
,过点![]() 作
作![]() 的切线交
的切线交![]() 的延长线于点
的延长线于点![]() .
.
(1)求证:![]() 为等腰三角形;
为等腰三角形;
(2)若![]() ,
,![]() 的半径为3,求
的半径为3,求![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
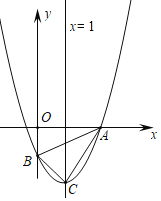
【题目】如图,对称轴为![]() 的抛物线
的抛物线![]() 与x轴交于点
与x轴交于点![]() 与y轴交于点B,顶点为C.
与y轴交于点B,顶点为C.
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 求
求![]() 的面积;
的面积;
![]() 若点P在x轴上,将线段BP绕着点P逆时针旋转
若点P在x轴上,将线段BP绕着点P逆时针旋转![]() 得到PD,点D是否会落在抛物线上?如果会,求出点P的坐标;若果不会,说明理由.
得到PD,点D是否会落在抛物线上?如果会,求出点P的坐标;若果不会,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
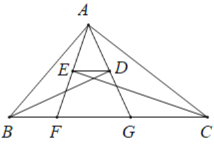
【题目】如图,已知BD⊥AG,CE⊥AF,BD、CE分别是∠ABC和∠ACB的角平分线,若BF=3,ED=2,GC=5,则△ABC的周长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图1,抛物线y=﹣![]() x2﹣
x2﹣![]() x+3与x轴交于A和B两点(点A在点B的左侧),与y轴相交于点C,点D的坐标是(0,﹣1),连接BC、AC
x+3与x轴交于A和B两点(点A在点B的左侧),与y轴相交于点C,点D的坐标是(0,﹣1),连接BC、AC

(1)求出直线AD的解析式;
(2)如图2,若在直线AC上方的抛物线上有一点F,当△ADF的面积最大时,有一线段MN=![]() (点M在点N的左侧)在直线BD上移动,首尾顺次连接点A、M、N、F构成四边形AMNF,请求出四边形AMNF的周长最小时点N的横坐标;
(点M在点N的左侧)在直线BD上移动,首尾顺次连接点A、M、N、F构成四边形AMNF,请求出四边形AMNF的周长最小时点N的横坐标;
(3)如图3,将△DBC绕点D逆时针旋转α°(0<α°<180°),记旋转中的△DBC为△DB′C′,若直线B′C′与直线AC交于点P,直线B′C′与直线DC交于点Q,当△CPQ是等腰三角形时,求CP的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)某中学学生为了解该校学生喜欢球类活动的情况,随机抽取了若干名学生进行问卷调查(要求每位学生只能填写一种自己喜欢的球类),并将调查的结果绘制成如下的两幅不完整的统计图.


请根据图中提供的信息,解答下面的问题:
(1)参加调查的学生共有 人,在扇形图中,表示“其他球类”的扇形的圆心角为 度;
(2)将条形图补充完整;
(3)若该校有2000名学生,则估计喜欢“篮球”的学生共有 人.
查看答案和解析>>
科目:初中数学 来源: 题型:
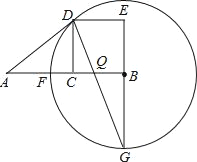
【题目】设C为线段AB的中点,四边形BCDE是以BC为一边的正方形.以B为圆心,BD长为半径的⊙B与AB相交于F点,延长EB交⊙B于G点,连接DG交于AB于Q点,连接AD.
求证:(1)AD是⊙B的切线;(2)AD=AQ;(3)BC2=CFEG.
查看答案和解析>>
科目:初中数学 来源: 题型:
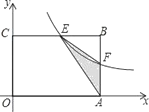
【题目】如图,在矩形OABC中,OA=6,OC=4,F是AB上的一个动点(F不与A,B重合),过点F的反比例函数![]() 的图象与BC边交于点E.
的图象与BC边交于点E.
(1)当F为AB的中点时,求该函数的解析式;
(2)当k为何值时,△EFA的面积最大,最大面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
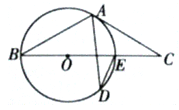
【题目】如图,BE是⊙O的直径,点A和点D是⊙O上的两点,过点A作⊙O的切线交BE延长线于点C
(I)若∠ADE=25°,求∠C的度数
(II)若AB=AC,求∠D的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com