
����Ŀ���ۺ���ʵ����
�����龳��
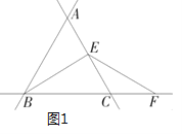
����ѧ�ۺ���ʵ�����ϣ�����ʦ��ʾ�������ֱ�ߡ��߶��Լ�����˶��任����̽���.�任�������£���ͼ 1��ֱ�� AB��AC��BC �����ཻ�� A��B��C ���㣬��֪��ABC�ǵȱ������Σ��� E ��ֱ�� AC ��һ���㣨�� E ����� A��C �غϣ����� F ��ֱ�� BC�ϣ����� BE��EF��ʹ EF=BE��


����˼����
��1������ʦ�������������һ�����⣺��ͼ 1����E���߶� AC ���е�ʱ��ȷ���߶� AE�� CF ��������ϵ������ֱ��д�����ۣ�AE____ CF������� ��������=����.
������⣺
��2�����ܶ���С���ܴ������������������⣺����E���߶� AC �ϵ�����һ�㣬�����������䣬��1���еĽ����Ƿ��������С����Ϊ������Ȼ�������������£���ͼ 2������ E�� ED��BC���� AB �ڵ� D. �����㲹������֤�����̣�
��չ���죺
��3�������ܡ�С������������ǣ�����E���˶�λ����ͼ3��ͼ4��ʾ�������������䣬�������ⲹȫͼ�Σ����ж��߶�AE��CF��������ϵ�Ƿ����仯�� ����ѡ������һ������֤��.


��4�������ġ�С������������ǣ����ȱߡ�ABC �ı߳�Ϊ![]() ��AE=1����BF �ij�Ϊ__________.������ֱ��д���������
��AE=1����BF �ij�Ϊ__________.������ֱ��д���������
���𰸡���1��������2������������3��û�з����仯��֤������������4��![]() ��
��![]()
��������
��1�����ݵȱ����������ʺ����ߺ�һ�õ�AE=CE����EBC=30������ECB=60�������ݵȱ߶ԵȽǿ�֪��EFC=��EBC=30��������������������ʵõ���ECB=��EFC+��FEC�����������FEC�����ݵȽǶԵȱߵõ�CE=CF�������õ����������ɽ������.
��2�����ݵȱ������ε����ʺ�ƽ���ߵ����ʵõ���ADE�ǵȱ������Σ�������֪BD=CE�����ݵȱ߶ԵȽǿ�֪��EFC=��EBC������������������ʵõ���EFC+��CEF=60������ϡ�DBE+��EBC=60�㣬����֤�á�DBE=��CEF������SAS֤�á�DBE�ա�CEF������ȫ�������ε����ʵõ�CF=DE�����ɵ�֤��
��3������ͼ3������E��ED��AB����BF�ڵ�D��ͬ��2���з���֤����BED�ա�FEC�����ɵ�֤������ͼ4������E��ED��BC����BA�ڵ�D��ͬ��2���з���֤����BED�ա�EFC�����ɵ�֤��
��4������ǰ���֤����֪������E��AC�ӳ�����ʱ��BF=BC+CF������E��AC��ʱ��BF=BC+CF������E��CA�ӳ�����ʱ��BF=BC-CF���ٽ��CF=AE�������BF.
��1��AE=CF
֤������ͼ1���ߡ�ABC�ǵȱ������Σ���E��AC�е�
��AE=CE����EBC=30������ECB=60��
��EF=BE
���EFC=��EBC=30��
�ߡ�ECB=��EFC+��FEC
���FEC=30��
��CE=CF
��AE=CF
�ʴ�Ϊ����
��2��
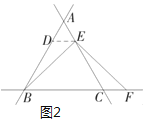
�ý�������Ȼ�������������£���ͼ 2������ E�� ED��BC���� AB �ڵ� D.
�ߡ�ABC�ǵȱ������Σ�
���ACB=��ABC=��BAC=60�㣬AB=AC=BC
��ED��BC��
���ADE=��AED=60��
���ADE�ǵȱ�������
��AD=AE=DE
��AB-AD=AC-AE����BD=CE
��BE=EF
���EBC=��EFC
�ߡ�DBE+��EBC=60��
��EFC+��CEF=60��
���DBE=��CEF
���DBE�ա�CEF��SAS��
��CF=DE
��CF=AE
��3����ͼ3��ʾ
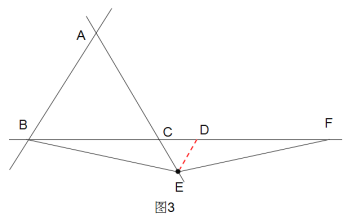
�߶�AE��CF��������ϵû�з����仯��
֤��������E��ED��AB����BF�ڵ�D
�ߡ�ABC�ǵȱ������Σ�
���ACB=��ABC=��BAC=60�㣬AB=AC=BC
��ED��AB��
���AED=��BAC=60�㣬��CDE=��ABC=60��
���ADE�ǵȱ�������
��CD=DE=CE
��AB-AD=AC-AE����BD=CE
��BE=EF
���EBC=��DFE
�ߡ�CBE+��CEB=��ACB=60��
��DEF+��DFE=��CDE=60��
���BEC=��DEF
���BEC+��CED=��DEF+��CED
����BED=��CEF
���BED�ա�FEC��SAS��
��BD=CF
��BD=BC+CD=AC+CE=AE
��CF=AE
��ͼ4��ʾ��
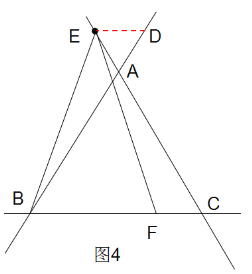
�߶�AE��CF��������ϵû�з����仯��
֤��������E��ED��BC����BA�ڵ�D
�ߡ�ABC�ǵȱ������Σ�
���ACB=��ABC=��BAC=60�㣬AB=AC=BC
��ED��BC��
���AED=��ACB=60�㣬��EDA=��ABC=60��
���ADE�ǵȱ�������
��AE=ED=AD
��AB+AD=AC+AE����BD=CE
��BE=EF
���EBC=��EFB
�ߡ�EBA+��ABC=��EBC
��FEC+��ACB=��EFB
���EBA=��FEC
���BED�ա�EFC��SAS��
��ED=FC
��CF=AE
��4������E��AC�ӳ�����ʱ��
��BF=BC+CF��CF=AE
��BF=BC+AE=![]()
����E��AC��ʱ��
��BF=BC+CF��CF=AE
��BF=BC+AE=![]()
����E��CA�ӳ�����ʱ��
��BF=BC-CF��CF=AE
��BF=BC-AE=![]()
����������BF=![]() ��
��![]()
�ʴ�Ϊ��![]() ��
��![]()



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
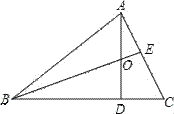
����Ŀ����ABC�У�AD��BC�ڵ�D��BE�ǡ�ABC��ƽ���ߣ���֪��ABC=40�㣬��C=60�㣬���AOB�Ķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�ؽ�����Ϊ�˷ḻ����ѧ���Ĵ�μ���Ҫ���ѧУ��չ��ʽ�����������������ij��ѧ����ѧ���������Ȥ�����������⣬��������˱�Уij���ѧ���������ݵ��������Ƴ����µIJ�����������ͳ��ͼ������ͳ��ͼ��

��1������ε����У�ϲ��������Ŀ��ͬѧ���� ���ˣ�������ͳ��ͼ�У���ƹ�������İٷֱ�Ϊ�� ��%�����ѧУ��800��ѧ��������ȫУѧ�������� ����ϲ��������Ŀ��
��2���뽫����ͳ��ͼ����������
��3���ڱ������ѧ���У�ϲ���������2��Ůͬѧ������Ϊ��ͬѧ����Ҫ���������ȡ2��ͬѧ�����༶�μ�У����ӣ���ֱ��д������ȡ��2��ͬѧǡ����1��Ůͬѧ��1����ͬѧ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
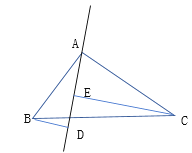
����Ŀ����ͼ���ڡ�ABC�У�AB=AC��DE�ǹ���A��ֱ�ߣ�BD![]() DE�ڵ�D�� CE
DE�ڵ�D�� CE![]() DE �ڵ� E.
DE �ڵ� E.
��1����BC��DE��ͬ��(��ͼ��ʾ������AD=CE����֤��![]()

��2����B��C�ڵ����ࣨ��ͼ��ʾ ���������������䣬AB��AC�Դ�ֱ�����������֤���������ǣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ��֯һ���֪ʶ�����������涨��ÿ���༶��2��������2��Ů����1����������ʦ��ɴ����ӣ�������ʱ��ÿ��ֻ����3����Ա�ϳ���������������ʦ����μӣ�����2����Ա�ֱ���2��������2��Ů���и�������1����������1�����ɼס���2�������ͱ�����2��Ů����1������������˴����ӣ���ǡ�ó鵽�������ס�Ů��������λ������һ���ϳ������ĸ��ʣ�������������״ͼ�������б��������о����ȷ��������������̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���ACB��90�㣬��ABC��30�㣬��CDE�ǵȱ������Σ���D�ڱ�AB�ϣ�

��1����ͼ1������E�ڱ�BC��ʱ����֤DE��EB��
��2����ͼ2������E�ڡ�ABC�ڲ�ʱ������ED��EB������ϵ��������֤����
��3����ͼ3������E�ڡ�ABC�ⲿʱ��EH��AB�ڵ�H������E��GE��AB�����߶�AC���ӳ����ڵ�G��AG��5CG��BH��3����CG�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͬѧ������ӦѧУ���٣����ü��ڲμ��˰༶��֯������ѧ����������ڲι�ij��ɫ����ʱ������վ��̨��DF�Ϸ����˶���ɽ��BC����һ�������ı�����AB������̨����F����ñ����ƶ���A������Ϊ![]() �������Ƶ�B������Ϊ
�������Ƶ�B������Ϊ![]() ����ͼ����̨֪��EFΪ3�ף�ɽ������BC�ij�Ϊ25�ף�ɽ��BC���¶�Ϊ1��
����ͼ����̨֪��EFΪ3�ף�ɽ������BC�ij�Ϊ25�ף�ɽ��BC���¶�Ϊ1��![]() ���������AB�ĸ߶�
���������AB�ĸ߶�![]() �����ȷ��
�����ȷ��![]() �ף��ο�����
�ף��ο�����![]() ��
��![]() ��
��![]()

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪a��b����ȡ��2����1��1��2������һ��ֵ��a��b������ֱ��y=ax+b��ͼ�����������ĸ������� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У���ACB��90����AB��5cm��BC��4cm������P�ӵ�A��������ÿ��1cm���ٶ�������A��B��C��A�˶������˶�ʱ��Ϊt��t��0���룮
��1��AC���� ��cm��
��2������Pǡ���ڡ�ABC�Ľ�ƽ�����ϣ����ʱt��ֵ��
��3�����˶������У���tΪ��ֵʱ����ACPΪ���������Σ�ֱ��д�������

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com