
【题目】如图,在正方形ABCD中,AB=5cm,E为对角线BD上一动点,连接AE、CE,过E点作EF⊥AE,交直线BC于点F,E点从B点出发,沿BD方向以每秒1cm的速度运动,当点E与点D重合时,运动停止.设△BEF的面积为ycm2,E点的运动时间为x秒.

(1)点E在整个运动过程中,试说明总有:CE=EF;
(2)求y与x之间关系的表达式,并写出x的取值范围.
【答案】(1)见解析;(2)y=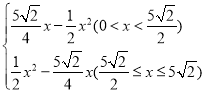
【解析】
(1)分两种情况:点F在BC的延长线上和在BC边上,在BC的延长线上时,作辅助线,构建三角形全等,证明△AEM≌△EFN和△ADE≌△CDE(SAS),可得AE=CE=EF;在BC边上时,同理可证明∠BAE=∠CFE,再证明△BEA≌△BEC得∠BAE=∠BCE,所以∠CFE=∠FCE,故可得结论;
(2)分两种情况:根据三角形的面积公式可得y与x之间关系的函数表达式,根据勾股定理计算BD的长可得x的取值.
(1)证明:如图1,过E作MN∥AB,交AD于M,交BC于N,
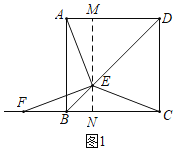
∵四边形ABCD是正方形,
∴AD∥BC,AB⊥AD,
∴MN⊥AD,MN⊥BC,
∴∠AME=∠FNE=90°=∠NFE+∠FEN,
∵AE⊥EF,
∴∠AEF=∠AEM+∠FEN=90°,
∴∠AEM=∠NFE,
∵∠DBC=45°,∠BNE=90°,
∴BN=EN=AM,
∴△AEM≌△EFN(AAS),
∴AE=EF,
∵四边形ABCD是正方形,
∴AD=CD,∠ADE=∠CDE,
∵DE=DE,
∴△ADE≌△CDE(SAS),
∴AE=CE,
∴CE=EF;
如图2,同理可证明∠BAE=∠CFE,

∵BD是正方形ABCD的对角线,
∴∠ABE=∠CBE=45°
又AB=CB,BE=BE
∴△BEA≌△BEC
∴∠BAE=∠BCE
∴∠CFE=∠FCE
∴CE=FE
因此,点E在整个运动过程中,总有:CE=EF;
(2)解:在Rt△BCD中,由勾股定理得:![]() ,
,
∴![]() ,
,
由题意得:BE=2x,
∴![]() ,
,
由(1)知:AE=EF=EC,
分两种情况:
①当![]() 时,如图3,
时,如图3,
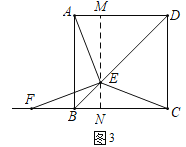
∵AB=MN=10,
∴ME=FN=10-![]() x,
x,
∴BF=FN-BN=10-![]() x-
x-![]() x=10-2
x=10-2![]() x,
x,
∴![]() ;
;
②当![]() 时,如图4,过E作EN⊥BC于N,
时,如图4,过E作EN⊥BC于N,
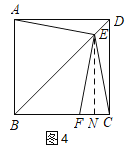
∴EN=BN=![]() x,
x,
∴FN=CN=10-![]() x,
x,
∴BF=BC-2CN=10-2(10-![]() x)=2
x)=2![]() x-10,
x-10,
∴![]() ;
;
综上,y与x之间关系的函数表达式为: y=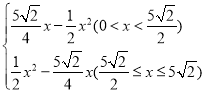


 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,对角线AC与BD相交于点O,点E,F分别为OB,OD的中点延长AE至G,使EG=AE,连接CG.
(1)求证:△ABE≌△CDF;
(2)当AB=![]() AC时,判断四边形EGCF是什么形状?请说明理由.
AC时,判断四边形EGCF是什么形状?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点 A(﹣2,0),B(2,0),C(0,2),点 D,点E分别是 AC,BC的中点,将△CDE绕点C逆时针旋转得到△CD′E′,及旋转角为α,连接 AD′,BE′.
(1)如图①,若 0°<α<90°,当 AD′∥CE′时,求α的大小;
(2)如图②,若 90°<α<180°,当点 D′落在线段 BE′上时,求 sin∠CBE′的值;
(3)若直线AD′与直线BE′相交于点P,求点P的横坐标m的取值范围(直接写出结果即可).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,点A1,B1,C1分别是BC、AC、AB的中点,A2,B2,C2分别是B1C1,A1C1,A1B1的中点,依此类推….若△ABC的周长为1,则△AnBnCn的周长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.

(1)CD与EF平行吗?为什么?
(2)如果∠1=∠2,且∠3=120°,求∠ACB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年10月17日是我国第五个“扶贫日”,某校学生会干部对学生倡导的“扶贫”自愿捐款活动进行抽样调查,得到一组学生捐款情况的数据,对学校部分捐款人数进行调查和分组统计后,将数据整理成如图所示的统计图,(图中信息不完整),已知A.B两组捐款人数的比为1:5.
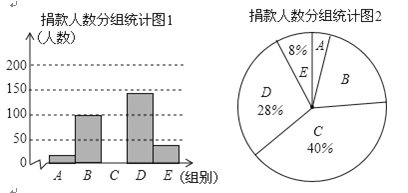
被调查的捐款人数分组统计表:
组别 | 捐款额x/元 | 人数 |
A | 1≤x<10 | a |
B | 10≤x<20 | 100 |
C | 20≤x<30 | ______ |
D | 30≤x<40 | ______ |
E | 40≤x | ______ |
请结合以上信息解答下列问题:
(1)求a的值和参与调查的总人数;
(2)补全“被调查的捐款人数分组统计图1”并计算扇形B的圆心角度数;
(3)已知该校有学生2200人,请估计捐款数不少于30元的学生人数有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知,BD与CE相交于点O,AD=AE,∠B=∠C,请解答下列问题:
(1)△ABD与△ACE全等吗?为什么?
(2)BO与CO相等吗?为什么?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com