
【题目】某校创建“环保示范学校”,为了解全校学生参加环保类社团的意愿,在全校随机抽取了50名学生进行问卷调查.问卷给出了五个社团供学生选择(学生可根据自己的爱好选择一个社团,也可以不选),对选择了社团的学生的问卷情况进行了统计,如下表:
社团名称 | A 酵素制作社团 | B 回收材料小制作社团 | C 垃圾分类社团 | D 环保义工社团 | E 绿植养护社团 |
人数 | 10 | 15 | 5 | 10 | 5 |
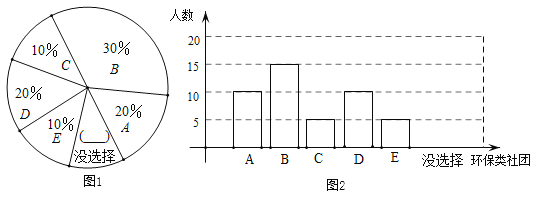
(1)根据以上信息填空:这5个数的中位数是______;扇形图中没选择的百分比为______;
(2)①补全条形统计图;②若该校有1400名学生,根据调查统计情况,请估计全校有多少学生愿意参加环保义工社团;
(3)若小诗和小雨两名同学在酵素制作社团或绿植养护社团中任意选择一个参加,请用树状图或列表法求出这两名同学同时选择绿植养护社团的概率.
【答案】(1)10,10%;(2)①见解析,②全校约有280名学生愿意参加环保义工社团;(3)见解析,![]() .
.
【解析】
对于(1),根据中位数的定义得到答案,利用各部分所占的百分比之和为1求出没有选择的百分比,
对于(2),①由(1)即可补全条形统计图,②利用样本估计总体的思想解决问题即可;
对于(3),画出树状图将所有可能出现的情况表示出来,再找出这两名同学同时选择绿植养护社团的情况,根据概率的公式得到答案.
解:(1)这5个数从小到大排列:5,5,10,10,15,故中位数为10.
没有选择的占1-10%-30%-20%-10%-20%=10%
故答案为:10;10%
(2)①补全条形图如下:②1400×20%=280(名),∴全校约有280名学生愿意参加环保义工社团;
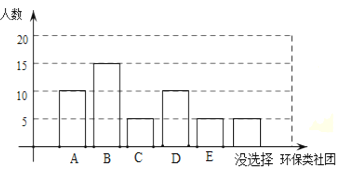
(3)酵素制作社团、绿植养护社团分别用A、B表示,画树状图如下:

由树状图知共有4种等可能结果,其中两人同时选择绿植养护社团只有一种情况,∴两人同时选择绿植养护社团的概率为![]() .
.


科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=2,与x轴的一个交点坐标为(4,0),其部分图象如图所示,下列结论:①抛物线一定过原点②方程ax2+bx+c=0(a≠0)的解为x=0或x=4,③a﹣b+c<0;④当0<x<4时,ax2﹣bx+c<0;⑤当x<2时,y随x增大而增大,其中结论正确的个数( )
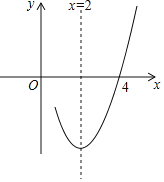
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数![]() ,(k为常数,k≠1).
,(k为常数,k≠1).
(1)若点A(1,2)在这个函数的图象上,求k的值;
(2)若在这个函数图象的每一分支上,y随x的增大而增大,求k的取值范围;
(3)若k=13,试判断点B(3,4),C(2,5)是否在这个函数的图象上,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
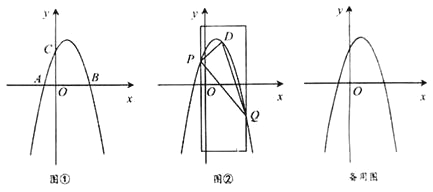
【题目】如图①,在平面直角坐标系xOy 中,抛物线y=ax2+bx+3经过点A(-1,0) 、B(3,0) 两点,且与y轴交于点C
.
(1)求抛物线的表达式;
(2)如图②,用宽为4个单位长度的直尺垂直于x轴,并沿x轴左右平移,直尺的左右两边所在的直线与抛物线相交于P、 Q两点(点P在点Q的左侧),连接PQ,在线段PQ上方抛物线上有一动点D,连接DP、DQ.
①若点P的横坐标为![]() ,求△DPQ面积的最大值,并求此时点D 的坐标;
,求△DPQ面积的最大值,并求此时点D 的坐标;
②直尺在平移过程中,△DPQ面积是否有最大值?若有,求出面积的最大值;若没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=3,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.则BG的长为( )
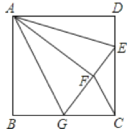
A. 1B. 2C. 1.5D. 2.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 是线段
是线段![]() 上一点,
上一点,![]() ,以点
,以点![]() 为圆心,
为圆心,![]() 的长为半径作⊙
的长为半径作⊙![]() ,过点
,过点![]() 作
作![]() 的垂线交⊙
的垂线交⊙![]() 于
于![]() ,
,![]() 两点,点
两点,点![]() 在线段
在线段![]() 的延长线上,连接
的延长线上,连接![]() 交⊙
交⊙![]() 于点
于点![]() ,以
,以![]() ,
,![]() 为边作
为边作![]() .
.
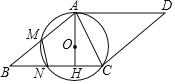
(1)求证:![]() 是⊙
是⊙![]() 的切线;
的切线;
(2)若![]() ,求四边形
,求四边形![]() 与⊙
与⊙![]() 重叠部分的面积;
重叠部分的面积;
(3)若![]() ,
,![]() ,连接
,连接![]() ,求
,求![]() 和
和![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了对学生进行革命传统教育,红旗中学开展了“清明节祭扫”活动.全校学生从学校同时出发,步行![]() 米到达烈士纪念馆.学校要求九
米到达烈士纪念馆.学校要求九![]() 班提前到达目的地,做好活动的准备工作.行走过程中,九(1)班步行的平均速度是其他班的
班提前到达目的地,做好活动的准备工作.行走过程中,九(1)班步行的平均速度是其他班的![]() 倍,结果比其他班提前
倍,结果比其他班提前![]() 分钟到达.分别求九(1)班、其他班步行的平均速度.
分钟到达.分别求九(1)班、其他班步行的平均速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】十八大以来,某校已举办五届校园艺术节.为了弘扬中华优秀传统文化,每届艺术节上都有一些班级表演“经典诵读”、“民乐演奏”、“歌曲联唱”、“民族舞蹈”等节目.小颖对每届艺术节表演这些节目的班级数进行统计,并绘制了如图所示不完整的折线统计图和扇形统计图.
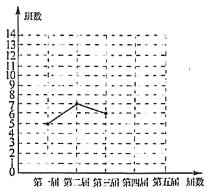
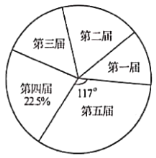
(1)五届艺术节共有________个班级表演这些节日,班数的中位数为________,在扇形统计图中,第四届班级数的扇形圆心角的度数为________;
(2)补全折线统计图;
(3)第六届艺术节,某班决定从这四项艺术形式中任选两项表演(“经典诵读”、“民乐演奏”、“歌曲联唱”、“民族舞蹈”分别用![]() ,
,![]() ,
,![]() ,
,![]() 表示).利用树状图或表格求出该班选择
表示).利用树状图或表格求出该班选择![]() 和
和![]() 两项的概率.
两项的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校组织全校1500名学生进行经典诗词诵背活动,为了解本次系列活动的效果,学校团委在活动开展一个月之后,随机抽取部分学生调查了“一周诗词诵背数量”,并根据调查结果绘制成如下的统计图1和图2.请根据相关信息,解答下列问题:
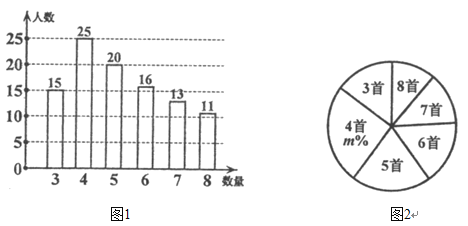
I.图2中的![]() 值为__________;
值为__________;
Ⅱ.求统计的这组数据的平均数、众数和中位数;
Ⅲ.估计此时该校学生一周诗词诵背6首(含6首)以上的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com