
����Ŀ��ijѧУ��֯ȫУ1500��ѧ�����о���ʫ���б����Ϊ�˽Ȿ��ϵ�л��Ч����ѧУ��ί�ڻ��չһ����֮�������ȡ����ѧ�������ˡ�һ��ʫ���б��������������ݵ��������Ƴ����µ�ͳ��ͼ1��ͼ2.����������Ϣ������������⣺
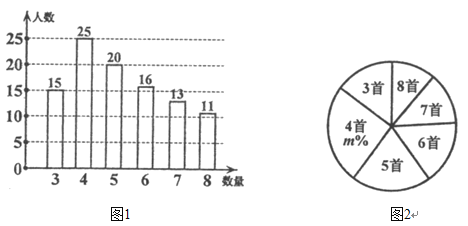
I.ͼ2�е�![]() ֵΪ__________��
ֵΪ__________��
��.��ͳ�Ƶ��������ݵ�ƽ��������������λ����
��.���ƴ�ʱ��Уѧ��һ��ʫ���б�6�ף���6�ף����ϵ�����.
���𰸡�I.25����.5.2,4,5����.600��.
��������
I. ���ֱ��ͼ�и��������ĺͼ�����òμ�ʫ���б�ѧ�����������ðٷֱȵ��������m��
��. ���ü�Ȩƽ������ʽ���ƽ������Ȼ��������������λ��������⣻
��. �������������Զ�Ӧ�İٷֱȼ�����⣮
�⣺I. �߲μ�ʫ���б�ѧ������Ϊ��15+25+20+16+13+11=100���ˣ�
��m![]()
��![]() .
.
��.��![]() .
.
���������ݵ�ƽ����Ϊ5.2.
�������������У�4������25�Σ����ֵĴ�����࣬
���������ݵ�����Ϊ4.
�߽��������ݰ���С�����˳�����У����д����м������������5��
���������ݵ���λ��Ϊ5.
��.���ƴ�ʱ��Уѧ��һ��ʫ���б�6�ף���6�ף����ϵ�����Ϊ��![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ����������ʾ��ѧУ����Ϊ�˽�ȫУѧ���μӻ��������ŵ���Ը����ȫУ�����ȡ��50��ѧ�������ʾ����飮�ʾ�������������Ź�ѧ��ѡ��(ѧ���ɸ����Լ��İ���ѡ��һ�����ţ�Ҳ���Բ�ѡ)����ѡ�������ŵ�ѧ�����ʾ����������ͳ�ƣ����±���
�������� | A ������������ | B ���ղ���С�������� | C ������������ | D �����幤���� | E ��ֲ�������� |
���� | 10 | 15 | 5 | 10 | 5 |
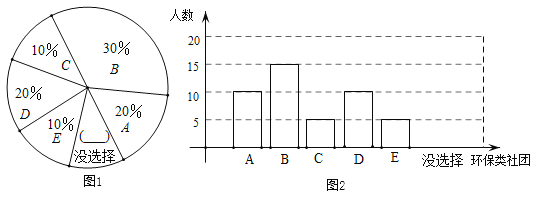
��1������������Ϣ��գ���5��������λ����______������ͼ��ûѡ��İٷֱ�Ϊ______��
��2���ٲ�ȫ����ͳ��ͼ��������У��1400��ѧ�������ݵ���ͳ������������ȫУ�ж���ѧ��Ը��μӻ����幤���ţ�
��3����Сʫ��С������ͬѧ�ڽ����������Ż���ֲ��������������ѡ��һ���μӣ�������״ͼ���б������������ͬѧͬʱѡ����ֲ���������ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(1)���ⷢ��
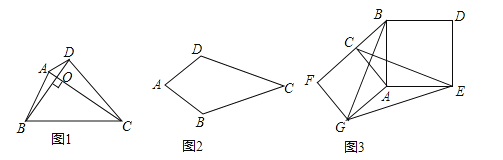
��ͼ1,��ACB����DCE��Ϊ����ֱ��������,��ACB=90��,B,C,D��һ��ֱ����.
���:�߶�AD,BE֮��Ĺ�ϵΪ .
(2)��չ̽��
��ͼ2,��ACB����DCE��Ϊ����ֱ��������,��ACB=��DCE=90��,���ж�AD,BE�Ĺ�ϵ,��˵������.
(3)�������
��ͼ3,�߶�PA=3,��B���߶�PA��һ��,PB=5,����AB,��AB�Ƶ�A��ʱ����ת90��õ��߶�AC,���ŵ�B��λ�õı仯,ֱ��д��PC�ķ�Χ.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
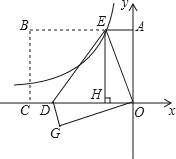
����Ŀ����ͼ����ֱ������ϵ�У�����OABC�Ķ���C��x��ĸ������ϣ���A��y���������ϣ�����OABC�����Ϊ8![]() ���Ѿ���OABC��DE���ۣ�ʹ��B���O�غϣ���C���ڵ�������G�㴦����EH��x����H����E��ķ���������y��
���Ѿ���OABC��DE���ۣ�ʹ��B���O�غϣ���C���ڵ�������G�㴦����EH��x����H����E��ķ���������y��![]() ͼ��ǡ�ù�DE���е�F����k��_____���߶�EH�ij�Ϊ��_____��
ͼ��ǡ�ù�DE���е�F����k��_____���߶�EH�ij�Ϊ��_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��깺���ס�������ͼ�鹲100�����ס�������ͼ��Ľ��۷ֱ�Ϊÿ��15Ԫ��35Ԫ���ס�������ͼ����ۼ۷ֱ�Ϊÿ��20Ԫ��45Ԫ��
��1������깺��ǡ������2300Ԫ�����ļס���ͼ������ٱ���
��2������ʱ����ͼ���8.5�ۣ���ͼ�鲻���ۣ����ס�������ͼ��ȫ�����������![]() �����ļס���ͼ������ٱ���
�����ļס���ͼ������ٱ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1���Խ����ഹֱ���ı��ν��������ı��Σ�
(1)�������⣺��ͼ2�����ı���![]() �У�
��![]() ��
��![]() �����ı���
�����ı���![]() �Ǵ����ı�������˵�����ɣ�
�Ǵ����ı�������˵�����ɣ�
(2)����̽������ͼ1���ı���![]() �ĶԽ���
�ĶԽ���![]() ��
��![]() ���ڵ�
���ڵ�![]() ��
��![]() ����֤����
����֤����![]() ��
��
(3)������⣺��ͼ3���ֱ���![]() ��ֱ�DZ�
��ֱ�DZ�![]() ��б��
��б��![]() Ϊ��������������
��������������![]() ��������
��������![]() ������
������![]() ��
��![]() ��
��![]() ����֪
����֪![]() ��
��![]() ����
����![]() �ij���
�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У�
��![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() ��
��![]() ���ڵ�
���ڵ�![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() ��
��![]() ���е㣬����
���е㣬����![]() ���ӳ���
���ӳ���![]() �ڵ�
�ڵ�![]() ��
��
��1����ͼ����ʾ����![]() ����֤��
����֤��![]() ��
��
��2����ͼ����ʾ����![]() ����ͼ����ʾ����
����ͼ����ʾ����![]() ����
����![]() ���
���![]() �غϣ��������߶�
�غϣ��������߶�![]() ��
��![]() ��
��![]() ֮������������������ϵ����ֱ��д����IJ��룬����֤����
֮������������������ϵ����ֱ��д����IJ��룬����֤����
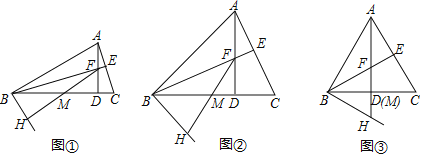
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Rt��OAB�Ķ���O������ԭ���غϣ���AOB=90����AO=2BO����A���ڷ���������![]() ��x>0����ͼ�����ƶ�ʱ��B����������ĺ�������ʽΪ�� ��
��x>0����ͼ�����ƶ�ʱ��B����������ĺ�������ʽΪ�� ��
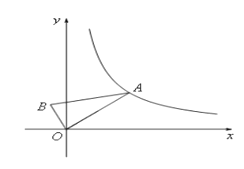
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����AOB����������A��O��B�ֱ�����������F1��![]() ��ͼ���ϣ���A�ĺ�����Ϊ��4����B��������Ϊ��2.(��A�ڵ�B�����)
��ͼ���ϣ���A�ĺ�����Ϊ��4����B��������Ϊ��2.(��A�ڵ�B�����)
(1)���A��B�����ꣻ
(2)����AOB�Ƶ�O��ʱ����ת90��õ���A'OB'��������F2��![]() ����A'��B'���㣬��֪��MΪ������F2�ĶԳ�����һ���㣬�ҵ�A'ǡ������OMΪֱ����Բ�ϣ�����OM��A'M�����OA'M�������
����A'��B'���㣬��֪��MΪ������F2�ĶԳ�����һ���㣬�ҵ�A'ǡ������OMΪֱ����Բ�ϣ�����OM��A'M�����OA'M�������
(3)��ͼ2���ӳ�OB'��������F2�ڵ�C������A'C�������������Ƿ���ڵ�D��ʹ����A��O��DΪ��������������OA'C����.�����ڣ��������D�����ꣻ�������ڣ���˵������.
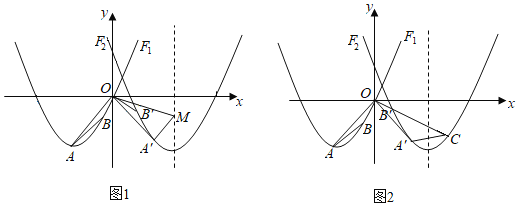
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com