
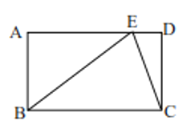
【题目】已知:如图,点E是矩形ABCD的边AD上一点,BE=AD,AE=8,现有甲乙二人同时从E点出发,分别沿EC、ED方向前进,甲的速度是乙的![]() 倍,甲到达点目的地C点的同时乙恰巧到达终点D处.
倍,甲到达点目的地C点的同时乙恰巧到达终点D处.
(1)求tan∠ECD的值
(2)求线段AB及BC的长度.
【答案】(1)![]() ;(2)AB=
;(2)AB=![]() ,BC=
,BC=![]()
【解析】
(1)设ED=x ,则EC=![]() x,在Rt△EDC中根据勾股定理用x表示出CD的长,由锐角三角函数的定义即可得出结论;
x,在Rt△EDC中根据勾股定理用x表示出CD的长,由锐角三角函数的定义即可得出结论;
(2)根据tan∠ECD=![]() ,设ED=x,CD=2x,表达出BE,再在Rt△ABE中,利用勾股定理得到AE2+AB2=BE2,列出方程解出x=
,设ED=x,CD=2x,表达出BE,再在Rt△ABE中,利用勾股定理得到AE2+AB2=BE2,列出方程解出x=![]() ,从而求出AB,BC的值即可
,从而求出AB,BC的值即可
解:(1)∵四边形ABCD是矩形,
∴∠D是直角.
根据条件:甲的速度是乙的![]() 倍,设ED=x ,则EC=
倍,设ED=x ,则EC=![]() x,
x,
∴在Rt△EDC中CD=![]() = 2x,
= 2x,
∴tan∠ECD=![]() =
=![]() .
.
(2)∵四边形ABCD是矩形,
∴设ED=x,AB=CD=2x.
∵BE=AD,AE=8,
∴BE=AD=8+x.
∵在Rt△ABE中,AE2+AB2=BE2
∴82+(2x)2=(8+x)2,
∴x=![]() ,或x=0(不合题意,舍)
,或x=0(不合题意,舍)
∴AB=2x=![]() ,BC=AD=8+x=
,BC=AD=8+x=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】商场今年2月份营业额为400万元,3月份的营业额比2月份增加10%,5月份的营业额达到633.6万元.若设商场3月份到5月份营业额的月平均增长率为x,则下面列出的方程中正确的是( )
A.633.6(1+x)2=400(1+10%)B.633.6(1+2x)2=400×(1010%)
C.400×(1+10%)(1+2x)2=633.6D.400×(1+10%)(1+x)2=633.6
查看答案和解析>>
科目:初中数学 来源: 题型:
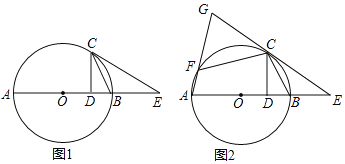
【题目】如图1,AB为⊙O的直径,C为⊙O上一点,连接CB,过C作CD⊥AB于点D,过点C作∠BCE,使∠BCE=∠BCD,其中CE交AB的延长线于点E.
(1)求证:CE是⊙O的切线.
(2)如图2,点F在⊙O上,且满足∠FCE=2∠ABC,连接AF井延长交EC的延长线于点G.
①试探究线段CF与CD之间满足的数量关系;
②若CD=4,BD=2,求线段FG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我校八年级有800名学生,在体育中考前进行一次排球模拟测试,从中随机抽取部分学生,根据其测试成绩制作了下面两个统计图,请根据相关信息,解答下列问题:

(1)本次抽取到的学生人数为________,图2中![]() 的值为_________.
的值为_________.
(2)本次调查获取的样本数据的平均数是__________,众数是________,中位数是_________.
(3)根据样本数据,估计我校八年级模拟体测中得12分的学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知抛物线y=![]() x2+bx+c经过点A(-1,0),B(5,0).
x2+bx+c经过点A(-1,0),B(5,0).

(1)求抛物线的解析式并写出顶点M的坐标;
(2)若点C在抛物线上,且点C的横坐标为8,求四边形AMBC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,并且关于x的一元二次方程ax2+bx+c﹣m=0有两个不相等的实数根,下列结论:①b2﹣4ac<0;②abc>0;③a﹣b+c<0;④m>﹣2,其中,正确的个数有( )

A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,E是BC的中点,连接DE、OE.
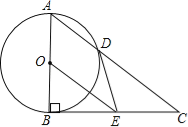
(1)判断DE与⊙O的位置关系并说明理由;
(2)若⊙O半径r=3,DE=4,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
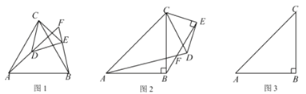
【题目】(1)如图1,△ABC和△CDE均为等边三角形,直线AD和直线BE交于点F.
①求证: AD=BE:
②求∠AFB的度数.
(2)如图2, △ABC和△CDE均为等腰直角三角形,∠ABC= ∠DEC=90°,直线AD和直线BE交于点F.
①求证: AD= ![]() BE:;
BE:;
②若AB=BC=3, DE=EC= 2,将△CDE绕着点C在平面内旋转,当点D落在线段BC上时,在图3中画出图形,并求BF的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工程队承接一铁路工程,在挖掘一条500米长的隧道时,为了尽快完成,实际施工时每天挖掘的长度是原计划的1.5倍,结果提前了25天完成了其中300米的隧道挖掘任务.
(1)求实际每天挖掘多少米?
(2)由于气候等原因,需要进一步缩短工期,要求完成整条隧道不超过70天,那么为了完成剩下的任务,在实际每天挖掘长度的基础上,至少每天还应多挖掘多少米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com