
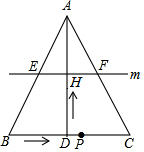
 如图,在△ABC中,AB=AC,AD⊥BC于点D,BC=10cm,AD=8cm.点P从点B出发,在线段BC上以每秒3cm的速度向点C匀速运动,与此同时,垂直于AD的直线m从底边BC出发,以每秒2cm的速度沿DA方向匀速平移,分别交AB、AC、AD于E、F、H,当点P到达点C时,点P与直线m同时停止运动,设运动时间为t秒(t>0).当t=$\frac{280}{183}$秒时,∠EPF=90°.
如图,在△ABC中,AB=AC,AD⊥BC于点D,BC=10cm,AD=8cm.点P从点B出发,在线段BC上以每秒3cm的速度向点C匀速运动,与此同时,垂直于AD的直线m从底边BC出发,以每秒2cm的速度沿DA方向匀速平移,分别交AB、AC、AD于E、F、H,当点P到达点C时,点P与直线m同时停止运动,设运动时间为t秒(t>0).当t=$\frac{280}{183}$秒时,∠EPF=90°. 分析 以BC边所在直线为x轴,DA边所在直线为y轴,点D为坐标原点建立直角坐标系,用含时间t的代数式表示出P点坐标,结合相似三角形的性质可表示出E、F点的坐标,根据两点间的距离公式表示出△EPF的三条边长,由勾股定理列出关于t的一元二次方程,解方程即可得出结论.
解答 解:以BC边所在直线为x轴,DA边所在直线为y轴,点D为坐标原点建立直角坐标系,如图所示.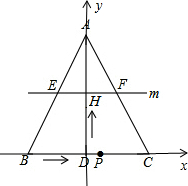
则点B(-5,0),点P(3t-5,0),点H(0,2t),点A(0,8),
∴AH=8-2t,BD=5,AD=8.
∵EF∥BC,
∴△AEH∽△ABD,
∴$\frac{EH}{BD}=\frac{AH}{AD}$,
∴EH=$\frac{5}{4}$(4-t),
∴点E的坐标为(-$\frac{5}{4}(4-t)$,2t),
同理点F的坐标为($\frac{5}{4}(4-t)$,2t).
由两点的间的距离公式可知:EF=$\frac{5}{2}$(4-t),PE=$\sqrt{[3t-5+\frac{5}{4}(4-t)]^{2}+(-2t)^{2}}$,PF=$\sqrt{[3t-5-\frac{5}{4}(4-t)]^{2}+(2t)^{2}}$,
∵∠EPF=90°,
∴有EF2=PE2+PF2,即$[\frac{5}{2}(4-t)]^{2}$=$[3t-5+\frac{5}{4}(4-t)]^{2}+(2t)^{2}$+$[3t-5-\frac{5}{4}(4-t)]^{2}+(2t)^{2}$,
解得:t=0(舍去),或t=$\frac{280}{183}$,
故答案为:$\frac{280}{183}$秒.
点评 本题考查了相似三角形的判定及性质、两点间的距离公式以及勾股定理,解题的关键是根据勾股定理得出关于t的一元二次方程.本题属于中档题,解题思路不难,但是数据较复杂,这就要求在解题中格外细心,以防丢分.


科目:初中数学 来源: 题型:选择题
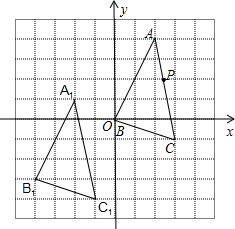 在如图的单位正方形网格中,三角形ABC经过平移后得到三角形A1B1C1,已知在AC上一点P($\frac{12}{5}$,2)平移后的对应点P1,则点P1的坐标为( )
在如图的单位正方形网格中,三角形ABC经过平移后得到三角形A1B1C1,已知在AC上一点P($\frac{12}{5}$,2)平移后的对应点P1,则点P1的坐标为( )| A. | (-$\frac{7}{5}$,-1) | B. | (-$\frac{3}{2}$,-2) | C. | (-$\frac{8}{5}$,-1) | D. | (-$\frac{12}{5}$,-1) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a=b=c | B. | a,b,c不全相等 | ||
| C. | a,b,c互不相等 | D. | 无法确定a,b,c之间关系 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com