
����Ŀ����֪��![]() ����С������������
����������������![]() ��
��![]() ����
����![]() ����ش����⣺
����ش����⣺
��1����ֱ��д��![]() ��
��![]() ��
��![]() ��ֵ��
��ֵ��![]() ��
��![]() ��
��![]() ��
��
��2��![]() ��
��![]() ��
��![]() ����Ӧ�ĵ�ֱ�Ϊ
����Ӧ�ĵ�ֱ�Ϊ![]() ��
��![]() ��
��![]() ����
����![]() Ϊһ���㣬���Ӧ����Ϊ
Ϊһ���㣬���Ӧ����Ϊ![]() ����
����![]() ��
��![]() ��
��![]() ֮���˶�ʱ���뻯��ʽ�ӣ�
֮���˶�ʱ���뻯��ʽ�ӣ�![]() ����д��������̣�
����д��������̣�
![]()
��3���ڣ�1����2���������£���![]() ��
��![]() ��
��![]() ��ʼ���������˶�������
��ʼ���������˶�������![]() ��ÿ��
��ÿ��![]() ����λ���ȵ��ٶ������˶���ͬʱ����
����λ���ȵ��ٶ������˶���ͬʱ����![]() �͵�
�͵�![]() �ֱ���ÿ��
�ֱ���ÿ��![]() ����λ���Ⱥ�
����λ���Ⱥ�![]() ����λ���ȵ��ٶ������˶������辭��
����λ���ȵ��ٶ������˶������辭��![]() ���ӹ�������
���ӹ�������![]() ���
���![]() ֮��ľ����ʾΪ
֮��ľ����ʾΪ![]() ����
����![]() ���
���![]() ֮��ľ����ʾΪ
֮��ľ����ʾΪ![]() �����ʣ�
�����ʣ�![]() ��ֵ�Ƿ�����ʱ��ı仯���ı䣿���仯����˵�����ɣ������䣬������ֵ��
��ֵ�Ƿ�����ʱ��ı仯���ı䣿���仯����˵�����ɣ������䣬������ֵ��
���𰸡���1��-1,1,6����2��-10����3�����䣬ֵΪ3��
��������
(1)������С����������1���Ƴ�b=1�������÷Ǹ������������a��c���ɣ�
(2)����ȷ��x�ķ�Χ���ٻ������ֵ���ɣ�
(3)BCAB��ֵ���䣮����������n��t��ʾ��BC��AB���ɽ�����⣮
�⣺��b����С����������
��b=1��
��(c6)2+|a+b|=0��(c6)20��|a+b|0��
��c=6��a=1��b=1��
�ʴ�Ϊ1��1��6;
��2����������1<x<1��
��|x+1||x1|2|x+5|��x+1+x12x10��10��
��3�����䣬
������BC��5+5nt2nt��5+3nt��AB��nt+2+2nt��2+3nt��
��BCAB��(5+3nt)(2+3nt)��3��
��BCAB��ֵ���䣬BCAB��3��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
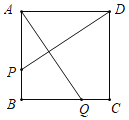
����Ŀ����ͼ����������ABCD�У�AB��8���ף��������P���߶�AB����2����/����ٶ���A����B���˶���ͬʱ����Q����1����/����ٶ��߶�BC����C����B���˶�������P����B��ʱ�����˶�����ֹͣ�����˶�ʱ��Ϊt�룬��AQ��DPʱ��t��ֵΪ_____�룮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
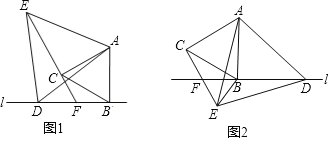
����Ŀ����֪�߶�AB��ֱ��l�ڵ�B����D��ֱ��l�ϣ��ֱ���AB��ADΪ�����ȱ�������ABC�͵ȱ�������ADE��ֱ��CE��ֱ��l�ڵ�F
��1������F���߶�BD��ʱ����ͼ1���߶�DF��CE��CF֮���������ϵ���� ����
��2������F���߶�DB���ӳ�����ʱ����ͼ2��
����1���е�������ϵ�Ƿ���Ȼ����������������д��֤�����̣�����������������д����ȷ�Ľ��ۣ���д��֤�����̣�
�����ȱߡ�ABC�͵ȱߡ�ADE�ı߳��ֱ���![]() ��
��![]() ��DF��3����BE�ij���
��DF��3����BE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪����AOB��90�㣬OCƽ�֡�AOB����P������OC�ϣ���E������OA�ϣ���F������OB�ϣ��ҡ�EPF��90�㣮
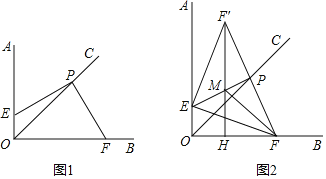
��1����ͼ1����֤��PE��PF��
��2����ͼ2������F����ֱ��EP�ĶԳƵ�F�䣬��F�����FH��OF��H������EF�䣬F��H��EP���ڵ�M������FM��ͼ�����EFM��ȵĽǹ����� ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��OPƽ�֡�AOB��PA��OA��PB��OB������ֱ�ΪA��B�����н����У���PA=PB����POƽ�֡�APB����OA=OB��AB��ֱƽ��OP��һ����������_________(�����)

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͬ���������ҹ��Ŵ�����Ȥ��֮һ����Լ�� 1500 ��ǰ���������㾭���оͼ����������Ȥ�����⣮���������������ģ�����������ͬ����������ʮ��ͷ�����о�ʮ���㣬�����ø����Σ������ľ仰����˼�ǣ�������ֻ������ͬ��һ��������������������� 35 ��ͷ�������������� 94 ֻ�� �������и��м�ֻ�����ã�������ɵ��� ��

A. �� 20 ֻ���� 15 ֻ B. �� 12 ֻ���� 23 ֻ
C. �� 15 ֻ���� 20 ֻ D. �� 23 ֻ���� 12 ֻ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���۲�ͼ�Σ�������⣺

��1�����±�����д����ʽ��д���еĿո�
ͼ�� | ͼ�� | ͼ�� | |
���������������Ļ� | 1������1����2=��2 | ����3��������4��������5��=��60 | �� �� |
���������������ĺ� | 1+����1��+2=2 | ����3��+����4��+����5��=��12 | �� �� |
����͵��� | ����2����2=��1 | �� �� | �� �� |
��2�������㷢�ֵĹ������ͼ���е���x��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1����ͼ�����ı��� ![]() �У�
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ����֤��
����֤��![]() ��
��

��2����ͼ������ˮ��߶�Ϊ ![]() �İ��ϣ�����������������������ʼʱ����
�İ��ϣ�����������������������ʼʱ���� ![]() �ij�Ϊ
�ij�Ϊ ![]() �ף�������
�ף������� ![]() ��ÿ����ٶ�������
��ÿ����ٶ�������![]() ����ƶ�����
����ƶ����� ![]() ��λ�ã��ʴ����ƶ��˶�����?������������ֱ�ģ�����������ţ���
��λ�ã��ʴ����ƶ��˶�����?������������ֱ�ģ�����������ţ���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������龳��ѧϰ��̽��ȫ������������������ʦ������������⣺��ͼ�٣���ABC�У���AB=12��AC=8����BC���ϵ�����AD��ȡֵ��Χ��ͬѧͨ�������������õ������µĽ���������ӳ�AD��E��ʹDE=AD������BE.����SAS��֤�õ���ADC����EDB���Ӷ������������ε����߹�ϵ�������AD��ȡֵ��Χ�� �����˼����Ŀ�г������е��������������������ɿ����ӳ����߹���ȫ�������Σ��ѷ�ɢ����֪����������֤�Ľ��ۼ��ϵ�ͬһ����������.
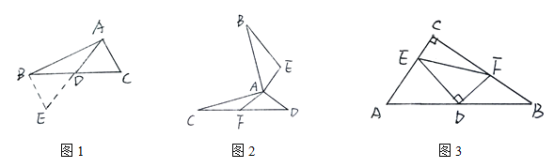
��ֱ�����ã���ͼ�ڣ�AB��AC��AD��AE��AB=AC��AD=AE��AF��ACD�ı�CD������.��֤��BE=2AF.
��������ã���ͼ�ۣ�����ABC�У���C=90����DΪAB���е㣬DE��DF��DE��AC�ڵ�E��DF��AB�ڵ�F������EF�����ж����߶�AE��BF��EFΪ�ߵ���������״����֤����Ľ���.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com