
分析 分别计算出两个不等式的解集,再根据大小小大中间找确定不等式组的解集即可,再找出解集范围内的整数即可.
解答 解:$\left\{\begin{array}{l}{x-3(x-2)≤4①}\\{x-1<\frac{1+2x}{3}②}\end{array}\right.$,
由①得:x≥1,
由②得:x<4,
在数轴上表示为: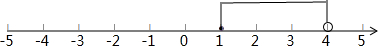 .
.
所以,不等式组的解集为:1≤x<4.
不等式组的整数解为1,2,3.
点评 此题主要考查了解一元一次不等式组,解决此类问题的关键在于正确解得不等式组或不等式的解集,然后再根据题目中对于解集的限制得到下一步所需要的条件,再根据得到的条件进而求得不等式组的整数解.声明:本试题解析著作权属


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
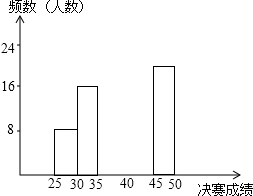 为增强学生的环保意识,某校组织学生开展了“雾霾天气知多少宣传暨竞赛活动”,经各班选拔,共推选出100名学会说呢过参加本次竞赛的决赛活动,决赛题设置了50道选择题,每答对一题得1分,满分50分,学校竞赛组委会经过统计,把这100名参赛学生的决赛成绩分成了5个组,并绘制出部分频数分布表和部分频数分布直方图如下:
为增强学生的环保意识,某校组织学生开展了“雾霾天气知多少宣传暨竞赛活动”,经各班选拔,共推选出100名学会说呢过参加本次竞赛的决赛活动,决赛题设置了50道选择题,每答对一题得1分,满分50分,学校竞赛组委会经过统计,把这100名参赛学生的决赛成绩分成了5个组,并绘制出部分频数分布表和部分频数分布直方图如下:| 组别 | 决赛成绩 x(分) | 频数(人数) |
| 第1组 | 25≤x<30 | 8 |
| 第2组 | 30≤x<35 | 16 |
| 第3组 | 35≤x<40 | 32 |
| 第4组 | 40≤x<45 | a |
| 第5组 | 45≤x<50 | 20 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com