
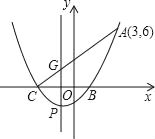
【题目】如图,一元二次方程x2+2x﹣3=0的两根x1,x2(x1<x2)是抛物线y=ax2+bx+c与x轴的两个交点C,B的横坐标,且此抛物线过点A(3,6).
(1)求此二次函数的解析式;
(2)设此抛物线的顶点为P,对称轴与线段AC相交于点G,则P点坐标为 ,G点坐标为 ;
(3)在x轴上有一动点M,当MG+MA取得最小值时,求点M的坐标.
【答案】(1)抛物线解析式为y=![]() x2+x﹣
x2+x﹣![]() ;(2)抛物线顶点P的坐标为(﹣1,﹣2),G点坐标为(﹣1,2);(3)M点坐标为(0,0)
;(2)抛物线顶点P的坐标为(﹣1,﹣2),G点坐标为(﹣1,2);(3)M点坐标为(0,0)
【解析】
(1)可先根据一元二次方程求出x1,x2的坐标,也就求出了B,C两点的坐标,然后可用交点式的二次函数通式来设二次函数的解析式,根据已知的A点的坐标求出二次函数的解析式.
(2)根据(1)二次函数解析式可得出顶点P的坐标和对称轴的解析式,G点就是直线AC与抛物线对称轴的交点,可先根据A,C的坐标,用待定系数法求出AC所在直线的解析式,然后将P点的横坐标代入求得的一次函数的解析式中即可求出G的坐标.
(3)本题的关键是先确定M点的位置,可先做A关于x轴的对称点A′然后连接A′C,与x轴的交点就是点M,那么可根据A′,C两点的坐标求出A′C所在直线的解析式,又已知了M在x轴上即可求出M点的坐标.
解:(1)解方程x2+2x﹣3=0
得x1=﹣3,x2=1.
∴抛物线与x轴的两个交点坐标为:C(﹣3,0),B(1,0),
设抛物线的解析式为y=a(x+3)(x﹣1).
∵A(3,6)在抛物线上,
∴6=a(3+3)(3﹣1),
∴a=![]() ,
,
∴抛物线解析式为y=![]() x2+x﹣
x2+x﹣![]() .
.
(2)由y=![]() x2+x﹣
x2+x﹣![]() =
=![]() (x+1)2﹣2,
(x+1)2﹣2,
∴抛物线顶点P的坐标为(﹣1,﹣2),对称轴方程为x=﹣1.
设直线AC的解析式为y=kx+b,
∵A(3,6),C(﹣3,0)在该直线上,
∴![]() ,
,
解得:k=1,b=3,
∴直线AC的解析式为:y=x+3.
将x=﹣1代入y=x+3
得y=2,
∴G点坐标为(﹣1,2).
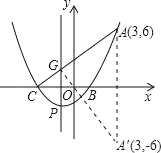
(3)作A关于x轴的对称点A′(3,﹣6),
连接A′G,A′G与x轴交于点M即为所求的点.
设直线A′G的解析式为y=kx+b.
∴![]() ,解得:
,解得:![]() ,
,
∴直线A′G的解析式为y=﹣2x,令x=0,则y=0.
∴M点坐标为(0,0).


科目:初中数学 来源: 题型:
【题目】某篮球运动员去年共参加![]() 场比赛,其中
场比赛,其中![]() 分球的命中率为
分球的命中率为![]() ,平均每场有
,平均每场有![]() 次
次![]() 分球未投中.
分球未投中.
![]() 该运动员去年的比赛中共投中多少个
该运动员去年的比赛中共投中多少个![]() 分球?
分球?
![]() 在其中的一场比赛中,该运动员
在其中的一场比赛中,该运动员![]() 分球共出手
分球共出手![]() 次,小明说,该运动员这场比赛中一定投中了
次,小明说,该运动员这场比赛中一定投中了![]() 个
个![]() 分球,你认为小明的说法正确吗?请说明理由.
分球,你认为小明的说法正确吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两种机器人都被用来搬运化工原料,A型机器人比B型机器人每小时多搬运30kg,A型机器人搬运900kg与B型机器人搬运600kg所用时间相等,两种机器人每小时分别搬运多少化工原料?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点D为
,点D为![]() 的中点,直角
的中点,直角![]() 绕点D旋转,
绕点D旋转,![]() ,
,![]() 分别与边
分别与边![]() ,
,![]() 交于E,F两点,下列结论:①
交于E,F两点,下列结论:①![]() 是等腰直角三角形;②
是等腰直角三角形;②![]() ;③
;③![]() ;④
;④![]() ,其中正确结论是( ).
,其中正确结论是( ).

A.①②④B.②③④C.①②③D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,已知
中,已知![]() ,
,![]() ,
,![]() 是
是![]() 的高,
的高,![]() ,
,![]() ,直线
,直线![]() ,动点
,动点![]() 从点
从点![]() 开始沿射线
开始沿射线![]() 方向以每秒
方向以每秒![]() 厘米的速度运动,动点
厘米的速度运动,动点![]() 也同时从点
也同时从点![]() 开始在直线
开始在直线![]() 上以每秒
上以每秒![]() 厘米的速度向远离
厘米的速度向远离![]() 点的方向运动,连接
点的方向运动,连接![]() 、
、![]() ,设运动时间为
,设运动时间为![]() 秒.
秒.

(1)请直接写出![]() 、
、![]() 的长度(用含有
的长度(用含有![]() 的代数式表示):
的代数式表示):![]() ______
______![]() ,
,![]() ______
______![]() ;
;
(2)当![]() 为多少时,
为多少时,![]() 的面积为
的面积为![]() ?
?
(3)请利用备用图探究,当![]() ___________秒时,
___________秒时,![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某数学兴趣小组为了测量河对岸l1的两棵古树A、B之间的距离,他们在河这边沿着与AB平行的直线l2上取C、D两点,测得∠ACB=15°,∠ACD=45°,若l1、l2之间的距离为50m,则古树A、B之间的距离为_____m.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下关于x的各个多项式中,a,b,c,m,n均为常数.
(1)根据计算结果填写下表:
二次项系数 | 一次项系数 | 常数项 | |
(2x + l)(x + 2) | 2 | 2 | |
(2x + 1)(3x - 2) | 6 | -2 | |
(ax + b)( mx + n) | am | bn |
(2)已知(x+ 3)2(x + mx +n)既不含二次项,也不含一次项,求m + n的值.
(3) 多项式M与多项式x2-3x + 1的乘积为2x4+ ax3 + bx2+ cx -3,则2 a +b + c的值为
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 经过点A(
经过点A(![]() ,0),B(
,0),B(![]() ,0),且与y轴相交于点C.
,0),且与y轴相交于点C.
(1)求这条抛物线的表达式;
(2)求∠ACB的度数;
(3)设点D是所求抛物线第一象限上一点,且在对称轴的右侧,点E在线段AC上,且DE⊥AC,当△DCE与△AOC相似时,求点D的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com