
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点D为
,点D为![]() 的中点,直角
的中点,直角![]() 绕点D旋转,
绕点D旋转,![]() ,
,![]() 分别与边
分别与边![]() ,
,![]() 交于E,F两点,下列结论:①
交于E,F两点,下列结论:①![]() 是等腰直角三角形;②
是等腰直角三角形;②![]() ;③
;③![]() ;④
;④![]() ,其中正确结论是( ).
,其中正确结论是( ).

A.①②④B.②③④C.①②③D.①②③④
【答案】C
【解析】
根据等腰直角三角形的性质可得∠CAD=∠B=45°,根据同角的余角相等求出∠ADF=∠BDE,然后利用“角边角”证明△BDE和△ADF全等,判断出③正确;根据全等三角形对应边相等可得DE=DF、BE=AF,从而得到△DEF是等腰直角三角形,判断出①正确;再求出AE=CF,判断出②正确;根据BE+CF=AF+AE,利用三角形的任意两边之和大于第三边可得BE+CF>EF,判断出④错误.
解:∵![]() ,
,![]() ,
,
∴△ABC是等腰直角三角形,∠C=∠B=45°,
∵点D为BC中点,
∴AD=CD=BD,AD⊥BC,∠CAD=45°,
∴∠CAD=∠B=45°,
∵∠MDN是直角,
∴∠ADF+∠ADE=90°,
∵∠BDE+∠ADE=∠ADB=90°,
∴∠ADF=∠BDE,
在△BDE和△ADF中,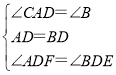 ,
,
∴△BDE≌△ADF(ASA),
故③正确;
∴DE=DF、BE=AF,
∴△DEF是等腰直角三角形,
故①正确;
∵AE=AB-BE,CF=AC-AF,
∴AE=CF,
故②正确;
∵BE+CF=AF+AE, AF+AE>EF,
∴BE+CF>EF,
故④错误;
综上所述,正确的结论有①②③;
故选:C.


 天天练口算系列答案
天天练口算系列答案科目:初中数学 来源: 题型:
【题目】观察与探究:
(1)观察下列各组数据并填空:
A:1,2,3,4,5,
平均数xA=________,方差sA2=________;
B:11,12,13,14,15,
平均数xB=________,方差sB2=________;
C:10,20,30,40,50,
平均数xC=________,方差sC2=________;
(2)分别比较A与B,C的计算结果,你能发现什么规律?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 上部分点的横坐标
上部分点的横坐标![]() ,纵坐标
,纵坐标![]() 的对应值如下表:
的对应值如下表:
| … |
|
|
|
|
| … |
| … |
|
|
|
|
| … |
小聪观察上表,得出下面结论:①抛物线与![]() 轴的一个交点为
轴的一个交点为![]() ;②函数
;②函数![]() 的最大值为
的最大值为![]() ;③抛物线的对称轴是
;③抛物线的对称轴是![]() ;④在对称轴左侧,
;④在对称轴左侧,![]() 随
随![]() 增大而增大.其中正确有( )
增大而增大.其中正确有( )
A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(观察)
51×49=(![]() )2﹣(
)2﹣(![]() )2
)2
102×98=(![]() )2﹣(
)2﹣(![]() )2
)2
2001×1999=(![]() )2﹣(
)2﹣(![]() )2
)2
(发现)根据阅读回答问题
(1)请根据上面式子的规律填空:
998×1002= 2﹣ 2
(2)在上述乘法运算中,设第一个因数为m,第二个因数为n,请用有m、n的符号语言写出你所发现的规律,并证明.
(应用)请运用(发现)中总结的规律计算:59.8×60.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的图象如图所示,则下列结论:①ac>0;②a-b+c<0;
的图象如图所示,则下列结论:①ac>0;②a-b+c<0;![]() 当
当![]() 时,
时,![]() ;
;![]() ,其中错误的结论有
,其中错误的结论有![]()
![]()
A. ②③ B. ②④ C. ①③ D. ①④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=2x2﹣4x﹣6.
(1)求这个二次函数图象的顶点坐标及对称轴;
(2)指出该图象可以看作抛物线y=2x2通过怎样平移得到?
(3)在给定的坐标系内画出该函数的图象,并根据图象回答:当x取多少时,y随x增大而减小;当x取多少时,y<0.
查看答案和解析>>
科目:初中数学 来源: 题型:
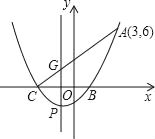
【题目】如图,一元二次方程x2+2x﹣3=0的两根x1,x2(x1<x2)是抛物线y=ax2+bx+c与x轴的两个交点C,B的横坐标,且此抛物线过点A(3,6).
(1)求此二次函数的解析式;
(2)设此抛物线的顶点为P,对称轴与线段AC相交于点G,则P点坐标为 ,G点坐标为 ;
(3)在x轴上有一动点M,当MG+MA取得最小值时,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某中学校园内有一块长为(3a+b)米,宽为(2a+b)米的长方形地块,学校计划在中间留一块边长为(a+b)米的正方形地块修建一座雕像,然后将阴影部分进行绿化.

(1)求绿化的面积.(用含a、b的代数式表示)
(2)当a=2,b=4时,求绿化的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com