
【题目】如图,在![]() 中,已知
中,已知![]() ,
,![]() ,
,![]() 是
是![]() 的高,
的高,![]() ,
,![]() ,直线
,直线![]() ,动点
,动点![]() 从点
从点![]() 开始沿射线
开始沿射线![]() 方向以每秒
方向以每秒![]() 厘米的速度运动,动点
厘米的速度运动,动点![]() 也同时从点
也同时从点![]() 开始在直线
开始在直线![]() 上以每秒
上以每秒![]() 厘米的速度向远离
厘米的速度向远离![]() 点的方向运动,连接
点的方向运动,连接![]() 、
、![]() ,设运动时间为
,设运动时间为![]() 秒.
秒.

(1)请直接写出![]() 、
、![]() 的长度(用含有
的长度(用含有![]() 的代数式表示):
的代数式表示):![]() ______
______![]() ,
,![]() ______
______![]() ;
;
(2)当![]() 为多少时,
为多少时,![]() 的面积为
的面积为![]() ?
?
(3)请利用备用图探究,当![]() ___________秒时,
___________秒时,![]() .
.
【答案】(1)![]() ,
,![]() ;(2)当
;(2)当![]() 为
为![]() 或
或![]() 时,
时,![]() 的面积为
的面积为![]() ;(3)
;(3)![]() .
.
【解析】
(1)根据“![]() ”即可得;
”即可得;
(2)根据![]() 可求出BD的长,因为要求t则需要求出CD的长,由点D的位置可知,需分点D在点B右侧和点D在点B左侧两种情况,根据线段的和与差分别讨论即可;
可求出BD的长,因为要求t则需要求出CD的长,由点D的位置可知,需分点D在点B右侧和点D在点B左侧两种情况,根据线段的和与差分别讨论即可;
(3)先假设![]() ,则有
,则有![]() ,同题(2)分两种情况讨论解出t的值,再检验两种情况下的t值,能否使得
,同题(2)分两种情况讨论解出t的值,再检验两种情况下的t值,能否使得![]() ,把不符合的舍去即可.
,把不符合的舍去即可.
(1)由“![]() ”得:
”得:![]()
故答案为:![]() ;
;
(2)![]() ,
,![]()
![]() ,为求CD的长分以下两种情况:
,为求CD的长分以下两种情况:
若![]() 在
在![]() 点右侧,
点右侧,![]() ,则
,则![]()
若![]() 在
在![]() 点左侧,
点左侧,![]() ,则
,则![]()
综上所述:当![]() 为
为![]() 或
或![]() 时,
时,![]() 的面积为
的面积为![]() ;
;
(3)如果![]() ,则有
,则有![]()
同题(2)分两种情况:
①若![]() 在
在![]() 点右侧,则
点右侧,则![]()
由![]() ,即
,即![]() 可得:
可得:![]()
检验:![]()
![]()
![]()
![]()
![]()
因此,由![]() 定理可得
定理可得![]()
②若![]() 在
在![]() 点左侧,则
点左侧,则![]()
由![]() ,即
,即![]() 可得:
可得:![]()
检验:![]()
![]()
![]()
![]()
![]()
![]()
因此,![]() 推不出
推不出![]()
综上,![]() 秒时,
秒时,![]() .
.


 优学名师名题系列答案
优学名师名题系列答案科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=﹣![]() x2+bx+c与x轴交于点A(﹣4,0),B(2,0),与y轴交于点C.请解答下列问题:
x2+bx+c与x轴交于点A(﹣4,0),B(2,0),与y轴交于点C.请解答下列问题:
(1)求抛物线的函数解析式并直接写出顶点M坐标;
(2)连接AM,N是AM的中点,连接BN,求线段BN长.
注:抛物线y=ax2+bx+c(a≠0)的顶点坐标是(﹣![]() ,
,![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(观察)
51×49=(![]() )2﹣(
)2﹣(![]() )2
)2
102×98=(![]() )2﹣(
)2﹣(![]() )2
)2
2001×1999=(![]() )2﹣(
)2﹣(![]() )2
)2
(发现)根据阅读回答问题
(1)请根据上面式子的规律填空:
998×1002= 2﹣ 2
(2)在上述乘法运算中,设第一个因数为m,第二个因数为n,请用有m、n的符号语言写出你所发现的规律,并证明.
(应用)请运用(发现)中总结的规律计算:59.8×60.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=2x2﹣4x﹣6.
(1)求这个二次函数图象的顶点坐标及对称轴;
(2)指出该图象可以看作抛物线y=2x2通过怎样平移得到?
(3)在给定的坐标系内画出该函数的图象,并根据图象回答:当x取多少时,y随x增大而减小;当x取多少时,y<0.
查看答案和解析>>
科目:初中数学 来源: 题型:
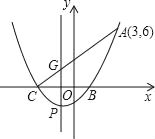
【题目】如图,一元二次方程x2+2x﹣3=0的两根x1,x2(x1<x2)是抛物线y=ax2+bx+c与x轴的两个交点C,B的横坐标,且此抛物线过点A(3,6).
(1)求此二次函数的解析式;
(2)设此抛物线的顶点为P,对称轴与线段AC相交于点G,则P点坐标为 ,G点坐标为 ;
(3)在x轴上有一动点M,当MG+MA取得最小值时,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,D、E分别是BC、AC上的动点且BD=CE,连接AD与BE相交于点F,连接CF,下列结论:①△ABD≌△BCE;②∠AFB=120°;③若BD=CD,则FA=FB=FC;④∠AFC=90°,则AF=3BF,其中正确的结论共有( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系xOy中,横坐标为a的点A在反比例函数y1═![]() (x>0)的图象上,点A′与点A关于点O对称,一次函数y2=mx+n的图象经过点A′.
(x>0)的图象上,点A′与点A关于点O对称,一次函数y2=mx+n的图象经过点A′.
(1)设a=2,点B(4,2)在函数y1、y2的图象上.
①分别求函数y1、y2的表达式;
②直接写出使y1>y2>0成立的x的范围;
(2)如图①,设函数y1、y2的图象相交于点B,点B的横坐标为3a,△AA'B的面积为16,求k的值;
(3)设m=![]() ,如图②,过点A作AD⊥x轴,与函数y2的图象相交于点D,以AD为一边向右侧作正方形ADEF,试说明函数y2的图象与线段EF的交点P一定在函数y1的图象上.
,如图②,过点A作AD⊥x轴,与函数y2的图象相交于点D,以AD为一边向右侧作正方形ADEF,试说明函数y2的图象与线段EF的交点P一定在函数y1的图象上.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学校组织的“文明出行”知识竞赛中,8(1)和8(2)班参赛人数相同,成绩分为A、B、C三个等级,其中相应等级的得分依次记为A级100分、B级90分、C级80分,达到B级以上(含B级)为优秀,其中8(2)班有2人达到A级,将两个班的成绩整理并绘制成如下的统计图,请解答下列问题:

(1)求各班参赛人数,并补全条形统计图;
(2)此次竞赛中8(2)班成绩为C级的人数为_______人;
(3)小明同学根据以上信息制作了如下统计表:
平均数(分) | 中位数(分) | 方差 | |
8(1)班 | m | 90 | n |
8(2)班 | 91 | 90 | 29 |
请分别求出m和n的值,并从优秀率和稳定性方面比较两个班的成绩;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com