
【题目】如图,抛物线y=ax2﹣2ax+m的图象经过点P(4,5),与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,且S△PAB=10.
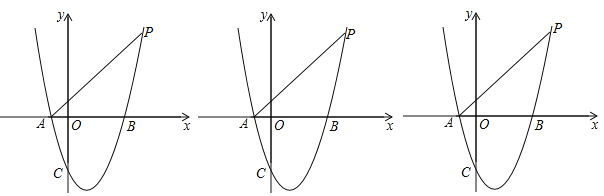
(1)求抛物线的解析式;
(2)在抛物线上是否存在点Q使得△PAQ和△PBQ的面积相等?若存在,求出Q点的坐标,若不存在,请说明理由;
(3)过A、P、C三点的圆与抛物线交于另一点D,求出D点坐标及四边形PACD的周长.
【答案】(1)y=x2﹣2x﹣3;(2)点Q的坐标为:(﹣2,5)或(﹣![]() ,﹣
,﹣![]() );(3)6
);(3)6![]() +4
+4![]() .
.
【解析】
(1)因为抛物线y=ax2﹣2ax+m,函数的对称轴为:x=1,S△PAB=10=![]() ×AB×yP=
×AB×yP=![]() AB×5,解得AB=4,即可求解;(2)分A、B在点Q(Q′)的同侧;点A、B在点Q的两侧两种情况,分别求解即可;(3)过点P作PO′⊥x轴于点O′,则点O′(4,0),则AO′=PO′=5,而CO′=5,故圆O′是过A、P、C三点的圆,即可求解.
AB×5,解得AB=4,即可求解;(2)分A、B在点Q(Q′)的同侧;点A、B在点Q的两侧两种情况,分别求解即可;(3)过点P作PO′⊥x轴于点O′,则点O′(4,0),则AO′=PO′=5,而CO′=5,故圆O′是过A、P、C三点的圆,即可求解.
解:
(1)y=ax2﹣2ax+m,函数的对称轴为:x=1,
S△PAB=10=![]() ×AB×yP=
×AB×yP=![]() AB×5,解得:AB=4,
AB×5,解得:AB=4,
故点A、B的坐标分别为:(﹣1,0)、(3,0),
抛物线的表达式为:y=a(x+1)(x﹣3),
将点P的坐标代入上式并解得:a=1,
故抛物线的表达式为:y=x2﹣2x﹣3…①;
(2)①当A、B在点Q(Q′)的同侧时,如图1,

△PAQ′和△PBQ′的面积相等,则点P、Q′关于对称轴对称,
故点Q′(﹣2,5);
②当A、B在点Q的两侧时,如图1,
设PQ交x轴于点E,分别过点A、B作PQ的垂线交于点M、N,
△PAQ和△PBQ的面积相等,则AM=BN,
而∠BEN=∠AEM,∠AME=∠BNE=90°,
∴△AME≌△BNE(AAS),
∴AE=BE,
即点E是AB的中点,则点E(1,0),
将点P、E的坐标代入一次函数表达式并解得:
直线PQ的表达式为:y=![]() x﹣
x﹣![]() …②,
…②,
联立①②并解得:x=﹣![]() 或4(舍去4),
或4(舍去4),
故点Q(﹣![]() ,﹣
,﹣![]() ),
),
综上,点Q的坐标为:(﹣2,5)或(﹣![]() ,﹣
,﹣![]() );
);
(3)过点P作PO′⊥x轴于点O′,则点O′(4,0),则AO′=PO′=5,而CO′=5,
故圆O′是过A、P、C三点的圆,
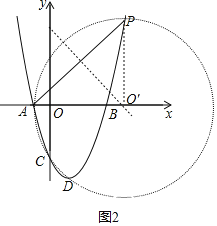
设点D(m,m2﹣2m﹣3),点O′(4,0),则DO′=5,
即(m﹣4)2+(m2﹣2m﹣3)2=25,
化简得:m(m+1)(m﹣1)(m﹣4)=0,
解得:m=0或﹣1或1或4(舍去0,﹣1,4),
故:m=1,
故点D(1,﹣4);
四边形PACD的周长=PA+AC+CD+PD=![]() .
.


科目:初中数学 来源: 题型:
【题目】“马航事件”的发生引起了我国政府的高度重视,我国政府迅速派出了舰船和飞机到相关海域进行搜寻.如图,在一次空中搜寻中,水平飞行的飞机在点A处测得前方海面的点F处有疑似飞机残骸的物体(该物体视为静止),此时的俯角为30°.为了便于观察,飞机继续向前飞行了800m到达B点,此时测得点F的俯角为45°.请你计算当飞机飞临F点的正上方点C时(点A,B,C在同一直线上),竖直高度CF约为多少米?(结果保留整数.参考数据:![]() ≈1.7)
≈1.7)

查看答案和解析>>
科目:初中数学 来源: 题型:
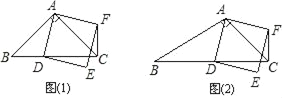
【题目】在△ABC中,∠ACB=45°.点D(与点B、C不重合)为射线BC上一动点,连接AD,以AD为一边且在AD的右侧作正方形ADEF.
(1)如果AB=AC.如图①,且点D在线段BC上运动.试判断线段CF与BD之间的位置关系,并证明你的结论.
(2)如果AB≠AC,如图②,且点D在线段BC上运动.(1)中结论是否成立,为什么?
(3)若正方形ADEF的边DE所在直线与线段CF所在直线相交于点P,设AC=4![]() ,BC=3,CD=x,求线段CP的长.(用含x的式子表示)
,BC=3,CD=x,求线段CP的长.(用含x的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是菱形ABCD的对角线BD上一点,连接CP并延长,交AD于点E,交BA的延长线于点F.

(1)求证:△APD≌△CPD;
(2)求证:△APE∽△FPA;
(3)若PE=2,EF=6,求PC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在水果销售旺季,某水果店购进一优质水果,进价为20元/千克,售价不低于20元/千克,且不超过32元/千克,根据销售情况,发现该水果一天的销售量y(千克)与该天的售价x(元/千克)满足如下表所示的一次函数关系.
销售量y(千克) | … | 34.8 | 32 | 29.6 | 28 | … |
售价x(元/千克) | … | 22.6 | 24 | 25.2 | 26 | … |
(1)某天这种水果的售价为23.5元/千克,求当天该水果的销售量.
(2)如果某天销售这种水果获利150元,那么该天水果的售价为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,tan∠ACB=2,D在△ABC内部,且AD=CD,∠ADC=90°,连接BD,若△BCD的面积为10,则AD的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校举办园博会知识竞赛,打算购买A、B两种奖品.如果购买A奖品10件、B奖品5件,共需120元;如果购买A奖品5件、B奖品10件,共需90元.
(1)A,B两种奖品每件各多少元?
(2)若购买A、B奖品共100件,总费用不超过600元,则A奖品最多购买多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
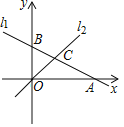
【题目】如图,在平面直角坐标系中,直线l1:y=﹣![]() x+1与x轴,y轴分别交于点A和点B,直线l2:y=kx(k≠0)与直线l1在第一象限交于点C.若∠BOC=∠BCO,则k的值为( )
x+1与x轴,y轴分别交于点A和点B,直线l2:y=kx(k≠0)与直线l1在第一象限交于点C.若∠BOC=∠BCO,则k的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 2
D. 2![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com