
【题目】某工厂计划生产![]() 、
、![]() 两种产品共60件,需购买甲、乙两种材料,生产一件
两种产品共60件,需购买甲、乙两种材料,生产一件![]() 产品需甲种材料4千克,乙种材料1千克;生产一件
产品需甲种材料4千克,乙种材料1千克;生产一件![]() 产品需甲、乙两种材料各3千克,经测算,购买甲、乙两种材料各1千克共需资金60元;购买甲种材料2千克和乙种材料3千克共需资金155元.
产品需甲、乙两种材料各3千克,经测算,购买甲、乙两种材料各1千克共需资金60元;购买甲种材料2千克和乙种材料3千克共需资金155元.
(1)甲、乙两种材料每千克分别是多少元?
(2现工厂用于购买甲、乙两种材料的资金不超过9900元,且生产![]() 产品不少于38件,问符合生产条件的生产方案有哪几种?
产品不少于38件,问符合生产条件的生产方案有哪几种?
(3)在(2)的条件下,若生产一件![]() 产品需加工费40元,若生产一件
产品需加工费40元,若生产一件![]() 产品需加工费50元,应选择哪种生产方案,使生产这60件产品的成本最低?(成本=材料费+加工费)
产品需加工费50元,应选择哪种生产方案,使生产这60件产品的成本最低?(成本=材料费+加工费)
【答案】(1)甲种材料每千克25元,乙种材料每千克35元;(2)共有如下三种方案:方案1、![]() 产品22个,
产品22个,![]() 产品38个,方案2、
产品38个,方案2、![]() 产品21个,
产品21个,![]() 产品39个,方案3、
产品39个,方案3、![]() 产品20个,
产品20个,![]() 产品40个;(3)生产
产品40个;(3)生产![]() 产品22件,
产品22件,![]() 产品38件成本最低.
产品38件成本最低.
【解析】
(1)设甲种材料每千克![]() 元,乙种材料每千克
元,乙种材料每千克![]() 元,根据题意列出方程,解方程即可;
元,根据题意列出方程,解方程即可;
(2)设生产![]() 产品
产品![]() 件,生产
件,生产![]() 产品
产品![]() 件.根据题意得出一元一次不等式组,解不等式组即可得出结果;
件.根据题意得出一元一次不等式组,解不等式组即可得出结果;
(3)设生产成本为![]() 元,根据题意得出
元,根据题意得出![]() 是
是![]() 的一次函数,即可得出结果.
的一次函数,即可得出结果.
解:(1)设甲种材料每千克![]() 元,乙种材料每千克
元,乙种材料每千克![]() 元,
元,
依题意得:![]() ,解得:
,解得:![]() ;
;
答:甲种材料每千克25元,乙种材料每千克35元.
(2)设生产![]() 产品
产品![]() 件,生产
件,生产![]() 产品
产品![]() 件.
件.
依题意得:![]()
解得:![]() ;
;
![]() 的值为非负整数,
的值为非负整数,
∴a=38、39、40;
答:共有如下三种方案:
方案1、![]() 产品22个,
产品22个,![]() 产品38个,
产品38个,
方案2、![]() 产品21个,
产品21个,![]() 产品39个,
产品39个,
方案3、![]() 产品20个,
产品20个,![]() 产品40个;
产品40个;
(3)生产![]() 产品22件,
产品22件,![]() 产品38件成本最低.理由如下:
产品38件成本最低.理由如下:
设生产成本为![]() 元,则
元,则![]() 与
与![]() 的关系式为:
的关系式为:
![]() ,
,
即![]() 是
是![]() 的一次函数,
的一次函数,
![]() ,
,
![]() 随
随![]() 增大而增大,
增大而增大,
![]() 当
当![]() 时,总成本最低;
时,总成本最低;
即生产![]() 产品22件,
产品22件,![]() 产品38件成本最低.
产品38件成本最低.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】山西民间的雕刻艺术源远流长,主要以古代传统吉祥纹样为素材,以石雕、木雕砖雕等形式,来体现主人的高尚情操和文化修养以及人们的美好愿望.某木雕经销商购进“木象”和“木马”两种雕刻艺术品,购“木象”艺术品共用了![]() 元,“木马”艺术品共用了
元,“木马”艺术品共用了![]() 元已知“木马”每件的进价比“木象”每件的进价贵
元已知“木马”每件的进价比“木象”每件的进价贵![]() 元,且购进“木象”“木马”的数量相同.
元,且购进“木象”“木马”的数量相同.

![]() 求每件“木象”、“木马”艺术品的进价;
求每件“木象”、“木马”艺术品的进价;
![]() 该经销商将购进的两种艺术品进行销售,“木象”的销售单价为
该经销商将购进的两种艺术品进行销售,“木象”的销售单价为![]() 元,“木马”的销售单价为
元,“木马”的销售单价为![]() 元,销售过程中发现“木象”的销量不好,经销商决定:“木象”销售一定数量后,将剩余的“木象”按原销售单价的七折销售;“木马”的销售单价保持不变要使两种艺术品全部售完后共获利不少于
元,销售过程中发现“木象”的销量不好,经销商决定:“木象”销售一定数量后,将剩余的“木象”按原销售单价的七折销售;“木马”的销售单价保持不变要使两种艺术品全部售完后共获利不少于![]() 元,问“木象”按原销售单价应至少销售多少件?
元,问“木象”按原销售单价应至少销售多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点P、Q分别是等边△ABC边AB、BC上的动点(端点除外),点P从顶点A、点Q从顶点B同时出发,且它们的运动速度相同,连接AQ、CP交于点M.
(1)求证:△ABQ≌△CAP;
(2)当点P、Q分别在AB、BC边上运动时,∠QMC变化吗?若变化,请说明理由;若不变,求出它的度数.
(3)如图2,若点P、Q在运动到终点后继续在射线AB、BC上运动,直线AQ、CP交点为M,则∠QMC变化吗?若变化,请说明理由;若不变,直接写出它的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ,
, ![]() 为实数).
为实数).
(![]() )当
)当![]() ,
, ![]() 取何值时,函数是二次函数.
取何值时,函数是二次函数.
(![]() )若它是一个二次函数,假设
)若它是一个二次函数,假设![]() ,那么:
,那么:
①它一定经过哪个点?请说明理由.
②若取该函数上横坐标满足![]() (
(![]() 为整数)的所有点,组成新函数
为整数)的所有点,组成新函数![]() .当
.当![]() 时,
时, ![]() 随
随![]() 的增大而增大,且
的增大而增大,且![]() 时是函数最小值,求
时是函数最小值,求![]() 满足的取值范围.
满足的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某无人机于空中A处探测到目标B、D的俯角分别是30°、60°,此时无人机的飞行高度AC为60m.随后无人机从A处继续水平飞行30![]() m到达A′处.
m到达A′处.
(1)求A、B之间的距离:
(2)求从无人机A′上看目标D的俯角的正切值
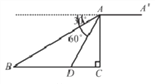
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AF∥CD,CB平分∠ACD,BD平分∠EBF,且BC⊥BD,下列结论:① BC平分∠ABE;② AC∥BE;③ ∠CBE+∠D=90°;④ ∠DEB=2∠ABC.其中正确结论的个数有( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线AB与x轴、y轴分别交于点A和点B,OA=4,且OA,OB长是关于x的方程x2﹣mx+12=0的两实根,以OB为直径的⊙M与AB交于C,连接CM,交x轴于点N,点D为OA的中点.
(1)求证:CD是⊙M的切线; (2)求线段ON的长.
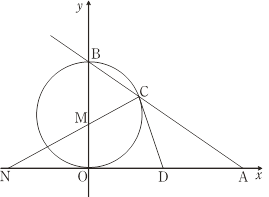
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某检修小组1乘一辆汽车沿公路检修线路,约定向东为正。某天从A地出发到收工时,行走记录为(单位:千米):+15,-2,+5,-1,+10,-3,-2,+12,+4,-5,+6。另一小组2也从A地出发,在南北向修,约定向北为正,行走记录为:-17,+9,-2,+8,+6,+9,-5,-1,+4,-7,-8.
(1)分别计算收工时,1,2两组在A地的哪一边,距A地多远?
(2)若每千米汽车耗油a升,求出发到收工各耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为建设美丽农村,村委会打算在正方形地块甲和长方形地块乙上进行绿化.在两地块内分别建造一个边长为![]() 的大正方形花坛和四个边长为
的大正方形花坛和四个边长为![]() 的小正方形花坛(阴影部分),空白区域铺设草坪,记
的小正方形花坛(阴影部分),空白区域铺设草坪,记![]() 表示地块甲中空白处铺设草坪的面积,
表示地块甲中空白处铺设草坪的面积, ![]() 表示地块乙中空白处铺设草坪的面积.
表示地块乙中空白处铺设草坪的面积.

(1)![]() __ ,
__ ,![]() (用含
(用含![]() 的代数式表示并化简) .
的代数式表示并化简) .
(2)若![]() ,求
,求![]() 的值.
的值.
(3)若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com