
【题目】已知函数![]() (
(![]() ,
, ![]() 为实数).
为实数).
(![]() )当
)当![]() ,
, ![]() 取何值时,函数是二次函数.
取何值时,函数是二次函数.
(![]() )若它是一个二次函数,假设
)若它是一个二次函数,假设![]() ,那么:
,那么:
①它一定经过哪个点?请说明理由.
②若取该函数上横坐标满足![]() (
(![]() 为整数)的所有点,组成新函数
为整数)的所有点,组成新函数![]() .当
.当![]() 时,
时, ![]() 随
随![]() 的增大而增大,且
的增大而增大,且![]() 时是函数最小值,求
时是函数最小值,求![]() 满足的取值范围.
满足的取值范围.
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为坐标原点,直线y=﹣x﹣3与x轴交于点A,与y轴交于点C,抛物线y=x2+bx+c经过A、C两点,与x轴交于另一点B
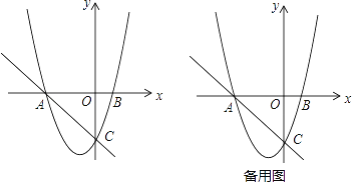
(1)求抛物线的解析式;
(2)点D是第二象限抛物线上的一个动点,连接AD、BD、CD,当S△ACD=![]() S四边形ACBD时,求D点坐标;
S四边形ACBD时,求D点坐标;
(3)在(2)的条件下,连接BC,过点D作DE⊥BC,交CB的延长线于点E,点P是第三象限抛物线上的一个动点,点P关于点B的对称点为点Q,连接QE,延长QE与抛物线在A、D之间的部分交于一点F,当∠DEF+∠BPC=∠DBE时,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某水渠的横断面是等腰梯形,已知其斜坡AD的坡度为1:1.2,斜坡BC的坡度为1:0.8,现测得放水前的水面宽EF为3.8米,当水闸放水后,水渠内水面宽GH为6米.则放水后水面上升的高度是( )米.
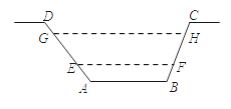
A. 1.2 B. 1.1 C. 0.8 D. 2.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,有一块长为![]() 米、宽为
米、宽为![]() 米的长方形空地,现计划将这块空地四周均留出2米宽修道路,中间用来绿化.
米的长方形空地,现计划将这块空地四周均留出2米宽修道路,中间用来绿化.
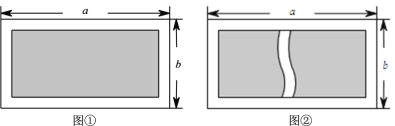
(1)求绿化的面积(用含![]() 、
、![]() 的代数式表示).
的代数式表示).
(2)若长方形空地的面积为576米2,周长为120米,求绿化的面积.
(3)若在图①的绿化部分再修一条2米宽道路,如图②,求绿化的面积(用含![]() 、
、![]() 的代数式表示).
的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,
,![]() ,点
,点![]() 是射线
是射线![]() 上一动点(与点
上一动点(与点![]() 不重合),
不重合),![]() 、
、![]() 分别平分
分别平分![]() 和
和![]() ,分别交射线
,分别交射线![]() 于点
于点![]() 、
、![]() .
.

(1)求![]() 的度数;
的度数;
(2)当点![]() 运动时,
运动时,![]() 与
与![]() 之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由;若变化,请写出变化规律.
之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由;若变化,请写出变化规律.
(3)当点![]() 运动到使时
运动到使时![]() ,求
,求![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂计划生产![]() 、
、![]() 两种产品共60件,需购买甲、乙两种材料,生产一件
两种产品共60件,需购买甲、乙两种材料,生产一件![]() 产品需甲种材料4千克,乙种材料1千克;生产一件
产品需甲种材料4千克,乙种材料1千克;生产一件![]() 产品需甲、乙两种材料各3千克,经测算,购买甲、乙两种材料各1千克共需资金60元;购买甲种材料2千克和乙种材料3千克共需资金155元.
产品需甲、乙两种材料各3千克,经测算,购买甲、乙两种材料各1千克共需资金60元;购买甲种材料2千克和乙种材料3千克共需资金155元.
(1)甲、乙两种材料每千克分别是多少元?
(2现工厂用于购买甲、乙两种材料的资金不超过9900元,且生产![]() 产品不少于38件,问符合生产条件的生产方案有哪几种?
产品不少于38件,问符合生产条件的生产方案有哪几种?
(3)在(2)的条件下,若生产一件![]() 产品需加工费40元,若生产一件
产品需加工费40元,若生产一件![]() 产品需加工费50元,应选择哪种生产方案,使生产这60件产品的成本最低?(成本=材料费+加工费)
产品需加工费50元,应选择哪种生产方案,使生产这60件产品的成本最低?(成本=材料费+加工费)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两城市之间开通了动车组高速列车。已知每隔2h有一列速度相同的动车组列车从甲城开往乙城。如图,OA是第一列动车组列车离开甲城的路程s(km)与运行时间t(h)的函数图象,BC是一列从乙城开往甲城的普通快车距甲城的路程s(km)与运行时间t(h)的函数图象。请根据图中的信息,解答下列问题:
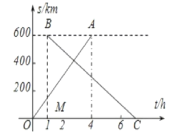
(1)从图象看,普通快车发车时间比第一列动车组列车发车时间___1h(填“早”或“晚”),点B的纵坐标600的实际意义是___;
(2)请直接在图中画出第二列动车组列车离开甲城的路程s(km)与时间t(h)的函数图象;
(3)若普通快车的速度为100km/h,
①求BC的表达式,并写出自变量的取值范围;
②第二列动车组列车出发多长时间后与普通快车相遇?
③请直接写出这列普通快车在行驶途中与迎面而来的相邻两列动车组列车相遇的时间间隔.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com