
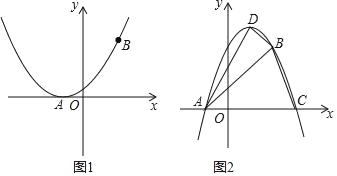
����Ŀ����֪�����ߵı���ʽ��y=ax2+��1��a��x+1��2a��aΪ������0�ij���������������������aΪ��ֵʼ�վ�������A�Ͷ���B��AΪx���ϵĵ㣬BΪ��һ�����ڵĵ㣮
��1����д��A��B��������꣺A���� ����0����B���� ������ ������
��2����ͼ1������������x��ֻ��һ��������ʱ����a��ֵ��
��3����ͼ2����a��0ʱ�������������߶�����D����x�����һ����Ϊ��C���ҵ�A��B��C��D��û����������غϣ�
�١�ABC�ܷ���ֱ�������Σ�Ϊʲô��
����ʹ�á�ABD��ֱ�������Σ��������a��ֵ�������1��a��ֵ���ɣ�
���𰸡���1����1��2��3����2��a=![]() ����3����a=��
����3����a=��![]() ����a=��1��
����a=��1��
��������
��1��y=ax2+��1-a��x+1-2a=a��x2-x-2��+x+1������x2-x-2��=0ʱ������aΪ��ֵʼ�վ�������A�Ͷ���B��������⣻
��2������������x��ֻ��һ��������ʱ����=0��������⣻
��3����A��-1��0������C��x��0����AB���ڵ�ֱ�ߵ�k1ֵΪ1��BC���ڵ�ֱ�ߵ�k2ֵΪ��![]() =3a����k1k2=-1������⣻���裺��ABD=90�����裺D��m��n��������Τ�ﶨ���ã�m2=-
=3a����k1k2=-1������⣻���裺��ABD=90�����裺D��m��n��������Τ�ﶨ���ã�m2=-![]() ����m=-
����m=-![]() ����y=ax2+��1-a��x+1-2a֪��m=
����y=ax2+��1-a��x+1-2a֪��m=![]() ������-
������-![]() =
=![]() ��������⣮
��������⣮
�⣺��1��y=ax2+��1��a��x+1��2a=a��x2��x��2��+x+1��
����x2��x��2��=0ʱ������aΪ��ֵʼ�վ�������A�Ͷ���B��
��x=��1��2����A����1��0����B��2��3����
�ʣ����ǩ�1��2��3��
��2������������x��ֻ��һ��������ʱ����=0��
������1��a��2��2a��1��2a��=0����ã�a=![]() ��
��
��3����A����1��0������C��x��0����
��Τ�ﶨ������1x=![]() ����C��
����C��![]() ��0����
��0����
AB���ڵ�ֱ�ߵ�k1ֵΪ1��
BC���ڵ�ֱ�ߵ�k2ֵΪ��![]() =3a��
=3a��
��k1k2=��1ʱ��AB��BC����ã�a=��![]() ��
��
���裺��ABD=90�㣬
��ֱ��BD����ֱ�߷��̵�k=��1����ֱ�߷���Ϊ��y=��x+5��
��ֱ��BD���ڵķ�������κ��������ã�
ax2+��2��a��x����4+2a��=0��
�裺D��m��n������B��2��3��
��Τ�ﶨ���ã�m2=��![]() ����m=��
����m=��![]() ��
��
��y=ax2+��1��a��x+1��2a֪��m=![]() ��
��
������![]() =
=![]() ��
��
��ã�a=��1��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��OABC��һ�ŷ���ƽ��ֱ������ϵ�еľ���ֽƬ��OΪԭ�㣬��A��x����������ϣ���C��y����������ϣ�OA=10��OC=8����OC����ȡһ��D����ֽƬ��AD���ۣ�ʹ��O����BC���ϵĵ�E������D��E��������꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�ڣ���֪��![]() ��������
��������![]() ����
����![]() ��������
��������![]() ��
��
��1��ͼ�е�![]() ��������________��
��������________��
��2����![]() ����
����![]() ��ԳƵĵ�
��ԳƵĵ�![]() ��������______���������ı���
��������______���������ı���![]() ��
��
��3�����ı���![]() �������
�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������L��y��![]() x2+bx��2��x���ཻ��A��B���㣨��A�ڵ�B����ࣩ������y���ཻ�ڵ�C���ҵ�A�������ǣ���1��0����
x2+bx��2��x���ཻ��A��B���㣨��A�ڵ�B����ࣩ������y���ཻ�ڵ�C���ҵ�A�������ǣ���1��0����
��1����������ߵĺ�������ʽ������D�����ꣻ
��2���ж���ABC����״���������ABC�������
��3�������������������ƽ�ƣ��õ�������L�䣬L����x���ཻ��A'��B�����㣨��A���ڵ�B������ࣩ������y���ཻ�ڵ�C����Ҫʹ��A'B��C������ABC�������ȣ����������������������ߵĺ�������ʽ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
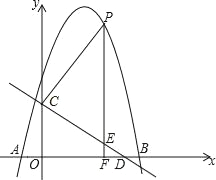
����Ŀ����ͼ��������y����x2+bx+c��x�ύ��A����1��0����B��5��0�����㣬ֱ��y����![]() x+3��y�ύ�ڵ�C����x�ύ�ڵ�D����P��ֱ��CD�Ϸ�����������һ���㣬����P��PF��x���ڵ�F����ֱ��CD�ڵ�E�����P�ĺ�����Ϊm��
x+3��y�ύ�ڵ�C����x�ύ�ڵ�D����P��ֱ��CD�Ϸ�����������һ���㣬����P��PF��x���ڵ�F����ֱ��CD�ڵ�E�����P�ĺ�����Ϊm��
(1)�������ߵĽ���ʽ��
(2)��PE�ij����ʱm��ֵ��
(3)Q��ƽ��ֱ������ϵ��һ�㣬��(2)������£���PQCDΪ������ı�����ƽ���ı����Ƿ���ڣ������ڣ�ֱ��д����Q�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
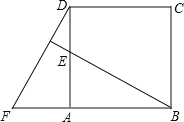
����Ŀ���ı���ABCD�������Σ���ADF��תһ���ǶȺ�õ���ABE����ͼ��ʾ�����AF��5��AB��9����
��1��ָ����ת���ĺ���ת�Ƕȣ�
��2����DE�ij��ȣ�
��3��BE��DF��λ�ù�ϵ��Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB=7��AC=6����A=45�㣬��D��E�ֱ��ڱ�AB��BC�ϣ�����BDE����DE����ֱ�߷��ۣ���B���ڵ�P����PD��PE�ֱ�AC�ڵ�M��N�����AD=2��PD��AB������Ϊ��D����ôMN�ij���_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������˶�Ավ�ڵ�O����ϰ�������O�����Ϸ�2 m��A�����������ɵ㣬�����еĸ߶�y(m)�����е�ˮƽ����x(m)�����ϵʽy��a(x��6)2��h.��֪������O���ˮƽ����Ϊ9 m���߶�Ϊ2.43 m���ı߽��O���ˮƽ����Ϊ18 m.
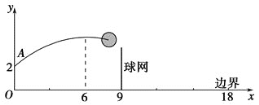
��1����h��2.6ʱ����y��x�Ĺ�ϵʽ(��Ҫ��д���Ա���x��ȡֵ��Χ)
��2����h��2.6ʱ�����ܷ�Խ��������������磿��˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com