
����Ŀ���з��̽�Ӧ���⣺10��1�գ���ֵ���ĸ��70�����գ���У��У������4����ʦ���ٵؼ�����Ⱥ�����Щ������Զ��������һ����ʦ��Ϊ־Ը�ߣ�����㳡��Ա�ļ������ɢ����ʦ������һ�����½���ʱ˵�������ǵIJ������������������˺�Ц�ݶ�����ָ�����ȷ�������н�ʱ��������һʧ�����й�֮������װ�׳������ı�ʱ���Ǿ�ȷ���룮�Ӷ���������������������������ľ���Ϊ96�ף����õ�ʱ���ǹ̶��ģ�ÿ��װ�׳����뱣֤36s֮��ͨ�����������ʱ������װ�׳�ͬʱ�Ӷ������������ҵ��ٶ��Ǽ�1.1��������֪�ҵ�����������ʱ�����ñȼ���ǰ3s����ô
��1�����ٶ���ÿ������ף������ȷ��1��/�룩��
��2��������װ�׳���˳����ɲ�����������˵�����ɣ�

���𰸡���1��3����2���ܣ�������
��������
��1����׳����ٶ�Ϊÿ��x�ף����ҳ����ٶ�Ϊÿ��1.1x�ף�����ʱ�䣽·�����ٶȽ���ҵ�����������ʱ�����ñȼ���ǰ3s�����ɵó�����x�ķ�ʽ���̣���֮������ɵó����ۣ�
��2������ʱ�䣽·�����ٶȿ�����׳�����ʱ�䣬��ϼס�����������ʱ��֮��Ĺ�ϵ������ҳ�����ʱ�䣬����36����бȽϺɵó����ۣ�
�⣺��1����׳����ٶ�Ϊÿ��x�ף����ҳ����ٶ�Ϊÿ��1.1x�ף�
�����⣬�ã� ![]() ��
��
��ã� ![]() ��
��
�����飬 ![]() ��ԭ���̵Ľ⣬�ҷ������⣬
��ԭ���̵Ľ⣬�ҷ������⣬
��![]() ��
��
�𣺼��ٶ�Լ��ÿ��3�ף�
��2��![]() ���룩��33��3��30���룩��
���룩��33��3��30���룩��
��33��36��30��36��
��������װ�׳���˳����ɲ�������


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�AB=AC����BAC=54������BAC��ƽ������AB�Ĵ�ֱƽ���߽��ڵ�O������C��EF��E��BC�ϣ�F��AC�ϣ��۵�����C���Oǡ���غϣ����OEC�Ķ����ǣ� ��

A.128��B.118��C.108��D.98��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������������ij�ֽ�����Ϊ20Ԫ/������Ʒʱ����30Ԫ/���۳���ÿ�����۳�100�������������������Ʒ���ۼ�ÿ����1Ԫ/�������������ͽ�����2����
��1��Ϊ��ʵ��ÿ��1600Ԫ������������Ӧ��������Ʒ���ۼ۶�Ϊ���٣�
��2����ÿ����Ʒ���ۼ�ΪxԪ��������������ΪyԪ��
����y��x֮��ĺ�����ϵʽ��
����۾ֹ涨����Ʒ���ۼ۲��ܳ���40Ԫ/��������Ϊ�˻����������Ӧ������Ʒ�ۼ۶�Ϊ���٣���������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��O�У�ABΪ�ң�ֱ��PO����O�ڵ�M��N��PO��AB��C������B��ֱ��BD������AD��BM��AP��
��1����֤��PM��AD��
��2������BAP=2��M����֤��PA�ǡ�O�����ߣ�
��3����AD=6��tan��M=![]() �����O��ֱ����
�����O��ֱ����
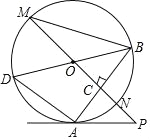
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����鳬���������ס���������ɫ��װʳƷ��800�����ס���������ɫ��װʳƷ�Ľ��ۺ��ۼ��������֪����2000Ԫ�������ִ�װʳƷ����������1600Ԫ�������ִ�װʳƷ��������ͬ��
�� | �� | |
���ۣ�Ԫ/���� | m | m��2 |
�ۼۣ�Ԫ/���� | 20 | 13 |
��1����m��ֵ��
��2�����繺���ļס���������ɫ��װʳƷȫ����������������������5200Ԫ���Ҳ�����5280Ԫ���ʸó����м��ֽ����������������ۼ۩����ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ��ǽ��AOB��OA��OB����OA��OB���Ȳ��ޣ��У�Ҫ��20m����ǽ����ֱ��ǽ��AOBΧ�ɵ���Ϊ���εĴ��֣��ҵ������AOBC�����Ϊ96m2��
��1����������AOBC�ij���
��2���й��Ϊ0.80��0.80��1.00��1.00����λ��m���ĵذ�ש���۷ֱ�Ϊ55Ԫ/���80Ԫ/�飬��ֻѡ����һ�ֵذ�ש��ǡ�����������ֵľ��ε��棨���Ʒ�϶��������һ�ֹ��ĵذ�ש���ý��٣�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ��,
(1) ȡ��M(1��0)�����M��ֱ��l�� ![]() �ľ���Ϊ_________��ȡֱ��
�ľ���Ϊ_________��ȡֱ��![]() ��ֱ��lƽ�У�����ֱ�߾���Ϊ_________.
��ֱ��lƽ�У�����ֱ�߾���Ϊ_________.
(2) ��֪��PΪ������y��x2��4x��x���Ϸ�һ�㣬�ҵ�P��ֱ��l�� ![]() �ľ���Ϊ
�ľ���Ϊ![]() �����P������.
�����P������.
(3) ��ֱ��y��kx��m��������y��x2��4x�ཻ��x���Ϸ�����A��B��A��B����ߣ����ҡ�AOB��90�㣬���P(2��0)��ֱ��y��kx��m�ľ�������ʱֱ��y��kx��m�Ľ���ʽ.


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��Rt��ABC�У���C=900��AD�ǡ�BAC�ĽǷ���.
��1����AB�ϵ�һ��OΪԲ�ģ�ADΪ����ͼ��������O������д������������ͼ�ۼ�����
��2�����ж�ֱ��BC���O��λ�ù�ϵ����֤����Ľ��ۣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x�ķ��̣�k��1��x2+��2k��3��x+k+1=0����������ȵ�ʵ����x1��x2��
��1����k��ȡֵ��Χ��
��2���Ƿ����ʵ��k��ʹ���̵���ʵ������Ϊ�෴����������ڣ����k��ֵ����������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com