
分析 作AE⊥BC于点E,DF⊥BC交BC的延长线于F,再根据四边形ABCD是平行四边形,求证△ABE≌△DCF,得出AE=DF,BE=CF,由勾股定理得AC2=AE2+EC2=AE2+(BC-BE)2,BD2=DF2+BF2=DF2+(BC+CF)2=AE2+(BC+BE)2,所以AC2+BD2=2(AB2+BC2)进而得出答案.
解答 证明:作AE⊥BC于点E,DF⊥BC交BC的延长线于F,
则∠AEB=∠DFC=90°.
∵四边形ABCD是平行四边形,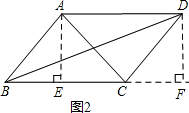
∴AB=DC,AB∥CD,
∴∠ABE=∠DCF,
在△ABE和△DCF中,
∵$\left\{\begin{array}{l}{∠AEB=∠DFC}\\{∠ABE=∠DCF}\\{AB=DC}\end{array}\right.$,
∴△ABE≌△DCF(AAS),
∴AE=DF,BE=CF.
在Rt△ACE和Rt△BDF中,由勾股定理,得
AC2=AE2+EC2=AE2+(BC-BE)2,
BD2=DF2+BF2=DF2+(BC+CF)2=AE2+(BC+BE)2,
∴AC2+BD2=2AE2+2BC2+2BE2=2(AE2+BE2)+2BC2.
又∵AE2+BE2=AB2,
∴AC2+BD2=2(AB2+BC2),
∵AB=a,BC=b,AC=m,BD=n,
即m2+n2=2(a2+b2).
点评 此题主要考查学生对勾股定理、平行四边形的性质和全等三角形的性质的理解和掌握,此题涉及到的知识点较多,综合性很强,有一定的拔高难度,属于难题.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
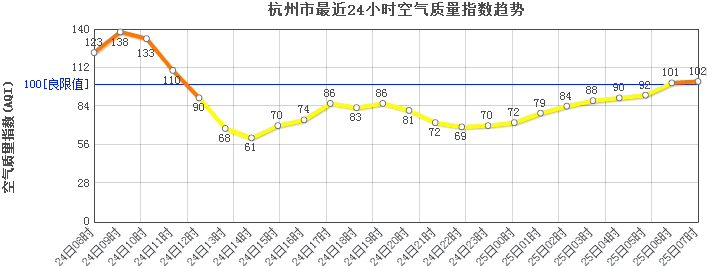
| A. | 在这个24小时中,AQI的值超过良限值时段是24日08时至24日12时 | |
| B. | 在这个24小时中,AQI对应的颜色为黄色的时段持续了20小时以上 | |
| C. | 在这个24小时中,AQI的最大值和最小值的差为77 | |
| D. | 建议中老年朋友在25日06时至07时进行晨练 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 购买香蕉数 | 不超过20千克 | 20千克以上 |
| 每千克价格 | 6元 | 5元 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com