
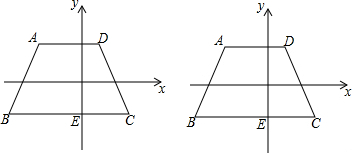
���� ��1����AF��BC����֪��C������BC=9�������CE=4��BE=5����֪����C������������B�����꣮��ֱ��AB�Ľ���ʽΪy=kx+b������֪���������������ʽ��
��2������Ҫ������������ۣ����ȵ�G���߶�BE���Ҳ����E�غϣ��ɵ�GE=5-t��S=��5-t����1��$\frac{1}{2}$����G���߶�CE���Ҳ����E�غϣ���ʱ��GE=t-5��S=��t-5����1��$\frac{1}{2}$���ֱ�����Ա�����ȡֵ��Χ���ɣ�
��3����ͼ�����GE�ij����G�������ɵõ�N�����꣬�����������õ��������ε����ʣ�������������ۣ�
��� 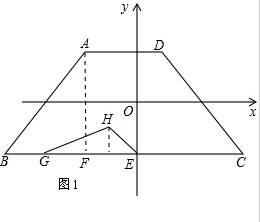 �⣺��1����ͼ1��
�⣺��1����ͼ1��
��BCƽ��x�ύy����E��BC=9��C��4��-2������BE=5��
��B��-5��-2����
��ֱ��AB�Ľ���ʽΪy=kx+b��
��$\left\{\begin{array}{l}{2=-2k+b}\\{-2=-5k+b}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{k=\frac{4}{3}}\\{b=\frac{14}{3}}\end{array}\right.$��
��ֱ��AB�Ľ���ʽΪy=$\frac{4}{3}$x+$\frac{14}{3}$��
��2����ͼ1��������ã�
����G���߶�BE���Ҳ����E�غϣ�
GE=5-t��
��S=��5-t����1��$\frac{1}{2}$=-$\frac{1}{2}$t+$\frac{5}{2}$����0��t��5����
����G���߶�CE���Ҳ����E�غϣ�
GE=t-5��
S=��t-5����1��$\frac{1}{2}$=$\frac{1}{2}$t-$\frac{5}{2}$��5��t��9����
��3������ͼ2����t=$\frac{7}{2}$��ʱ��
GE=5-$\frac{7}{2}$=$\frac{3}{2}$��
��G��-$\frac{3}{2}$��-2����
��ֱ�ߵ�GH�Ľ���ʽΪ��y=2x+1��
��x=0����y=1��
��N��0��1��
����H��-1��-1����N��0��1����
���ֱ��HN�Ľ���ʽΪ��y=2x+1��
��ֱ��HN��x��Ľ��㣨-$\frac{1}{2}$��0����
��HN�Ĵ�ֱƽ���߾�����-$\frac{1}{2}$��0����
�������ʽΪ��y=-$\frac{1}{2}x-\frac{1}{4}$��
���AB����P1�����BC����P2��
�ⷽ����$\left\{\begin{array}{l}{y=\frac{4}{3}x+\frac{14}{3}}\\{y=-\frac{1}{2}x-\frac{1}{4}}\end{array}\right.$�����$\left\{\begin{array}{l}{x=-\frac{59}{22}}\\{y=\frac{12}{11}}\end{array}\right.$��
��P1B=$\frac{85}{22}$��
��P1H=P1Nʱ����P�˶���P1����
��t1=$\frac{85}{22}$��
���BC����p2��
�ⷽ����
$\left\{\begin{array}{l}{y=-2}\\{y=-\frac{1}{2}x-\frac{1}{4}}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{x=\frac{7}{2}}\\{y=-2}\end{array}\right.$��
��t2=$\frac{27}{2}$
��AB=$\sqrt{{��5-2��}^{2}{+��2+2��}^{2}}$=5��CD=$\sqrt{{��4-1��}^{2}{+��2+2��}^{2}}=5$��
HN=$\sqrt{5}$��
��P3N=HNʱ����A���P3�غϣ�
��t3=5��
��P4N=HN=$\sqrt{5}$ʱ��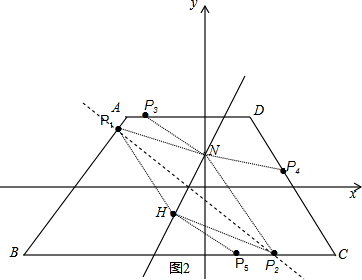
��ֱ��CD�Ľ���ʽΪ��$y=-\frac{4}{3}x+\frac{10}{3}$��
��P4[x����$-\frac{4}{3}x+\frac{10}{3}$��]
��${x}^{2}{+��-\frac{4}{3}x+\frac{10}{3}-1��}^{2}=5$��
��ã�x1=$\frac{28+6\sqrt{19}}{25}$������������ȥ����x2=$\frac{28-6\sqrt{19}}{25}$������������ȥ����
�����BC�ཻʱ��
p5H=NH=$\sqrt{5}$ʱ��
��ֱ��BC�Ľ���ʽΪ��y=-2��
p5��x��-2����
��x2+��-2-1��2=5��
��ã�x=$\sqrt{5}$��x=-$\sqrt{5}$����ȥ����
��t5=17-$\sqrt{5}$��
����������������t��ֵΪ��
t1=$\frac{85}{22}$��t2=$\frac{27}{2}$��t3=5��t4=17-$\sqrt{5}$��
���� ���⿼���һ�κ��������ü��ֶκ��������ã�����һ�κ�������ʽ�����������ε����ʣ����÷�������˼���ǽ������Ĺؼ���


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
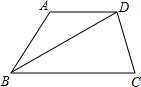 ��ͼ��������ABCD�У�AD��BC��AD=AB��BC=BD����A=140�㣬���C���ڣ�������
��ͼ��������ABCD�У�AD��BC��AD=AB��BC=BD����A=140�㣬���C���ڣ�������| A�� | 75�� | B�� | 60�� | C�� | 70�� | D�� | 80�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����

| A�� | 4�� | B�� | 3�� | C�� | 2�� | D�� | 1�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com