
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
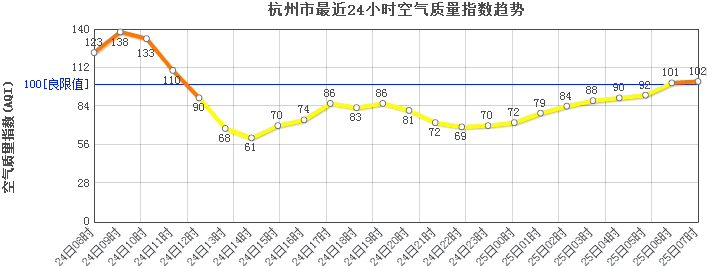
| A. | 在这个24小时中,AQI的值超过良限值时段是24日08时至24日12时 | |
| B. | 在这个24小时中,AQI对应的颜色为黄色的时段持续了20小时以上 | |
| C. | 在这个24小时中,AQI的最大值和最小值的差为77 | |
| D. | 建议中老年朋友在25日06时至07时进行晨练 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{{{({-2.5})}^2}}={({\sqrt{2.5}})^2}$ | B. | $\sqrt{a^2}=a$ | C. | $\sqrt{{x^2}-2x+1}=x-1$ | D. | $\sqrt{{x^2}-9}=\sqrt{x-3}•\sqrt{x+3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com