
【题目】如图,已知一次函数y=﹣![]() x+6的图象与坐标轴交于A、B两点,AE平分∠BAO,交x轴于点E.
x+6的图象与坐标轴交于A、B两点,AE平分∠BAO,交x轴于点E.
(1)求点B的坐标及直线AE的表达式;
(2)过点B作BF⊥AE,垂足为F,在y轴上有一点P,使线段PE+PF的值最小,求点P的坐标;
(3)若将已知条件“AE平分∠BAO,交x轴于点E”改变为“点E是线段OB上的一个动点(点E不与点O、B重合)”,过点B作BF⊥AE,垂足为F,以EF为边作正方形EFMN,当点M落在坐标轴上时,求E点坐标.
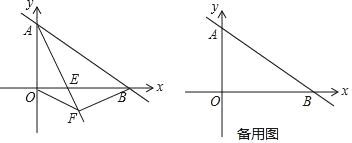
【答案】(1)B(8,0),y=﹣2x+6;(2)P(0,﹣![]() );(3)点E坐标为(
);(3)点E坐标为(![]() ,0)或(6,0).
,0)或(6,0).
【解析】
(1)设OE=x,作EM⊥AB于M.在Rt△EBM中,根据EM2+BM2=EB2,可得x2+42=(8-x)2,求出x即可解决问题;
(2)如图2中,作点E关于y轴的对称点E′,连接FE′交y轴于P,此时PE+PF的值最小.想办法切线直线FE′的解析式即可解决问题;
(3)①如图3中,当点M在y轴上时,作FP⊥OB于P,FQ⊥OM于Q.利用全等三角形的性质,证明四边形OPFQ是正方形即可解决问题;②如图4中,当点M在x轴上时,易知OA=OE=6,可得E(6,0).
(1)如图1中,
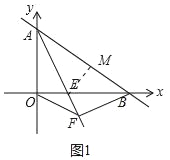
∵一次函数y=﹣![]() x+6的图象与坐标轴交于A、B点,
x+6的图象与坐标轴交于A、B点,
∴A(0,6),B(8,0),设OE=x,作EM⊥AB于M.
∵AE平分∠OAB,OE⊥OA,
∴OE=EM=x,
在△AEO和△AEM中,![]() ,
,
∴△AEO≌△AEM,
∴AM=AO=6,
∵OA=6,OB=8,∠AOB=90°,
∴AB=![]() =
=![]() =10,
=10,
∴BM=4,
在Rt△EBM中,∵EM2+BM2=EB2,
∴x2+42=(8﹣x)2,
∴x=3,
∴E(3,0),
设直线AE的解析式为y=kx+b,
则![]() ,
,
解得![]() ,
,
∴直线AE的解析式为y=﹣2x+6;
(2)如图2中,作点E关于y轴的对称点E′,连接FE′交y轴于P,此时PE+PF的值最小.
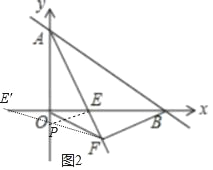
∵BF⊥AE,
∴直线BF的解析式为y=![]() x﹣4,
x﹣4,
由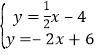 解得
解得![]() ,
,
∴F(4,﹣2),
∴直线FE′的解析式为y=﹣![]() x﹣
x﹣![]() ,
,
∴P(0,﹣![]() ).
).
(3)①如图3中,当点M在y轴上时,作FP⊥OB于P,FQ⊥OM于Q.

∵四边形EFMN是正方形,
∴FE=FM,∠EFM=∠PFQ,
∴∠EFP=∠MFQ,
∵∠FPE=∠FQM=90°,
∴△FPE≌△FQM,
∴FP=FQ,四边形OPFQ是正方形,设边长为x.
∵∠AEO=∠BEF,∠AOE=∠PFE=90°,
∴∠FAQ=∠FBP,
∵∠AQF=∠BPF=90°,
∴△AQF≌△BPF,
∴AQ=BP,
∴6+x=8﹣x
∴x=1,
∴F(1,﹣1),
∴直线AF的解析式为y=﹣7x+6,
∴E(![]() ,0);
,0);
②如图4中,当点M在x轴上时,易知OA=OE=6,可得E(6,0).
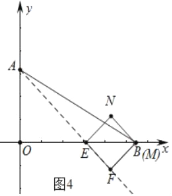
综上所述,满足条件的点E坐标为(![]() ,0)或(6,0).
,0)或(6,0).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图所示,BC是圆O的直径,点A,F在圆O上,连接AB,BF. 
(1)如图1,若点A、F把半圆三等分,连接OA,OA与BF交于点E.求证:E为OA的中点;
(2)如图2,若点A为弧 ![]() 的中点,过点A作AD⊥BC,垂足为点D,AD与BF交于点G.求证:AG=BG.
的中点,过点A作AD⊥BC,垂足为点D,AD与BF交于点G.求证:AG=BG.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为x=1,且抛物线经过A(﹣1,0)、C(0,﹣3)两点,与x轴交于另一点B.
(1)求这条抛物线所对应的函数关系式;
(2)在抛物线的对称轴x=1上求一点M,使点M到点A的距离与到点C的距离之和最小,并求出此时点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,下面不能判断是平行四边形的是( )

A. ∠B=∠D,∠A=∠C;
B. AB∥CD,AD∥BC
C. ∠B+∠DAB=180°,∠B+∠BCD=180°
D. AB∥CD,AB=CD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,∠A=70°,将平行四边形ABCD绕点B顺时针旋转到平行四边形A1BC1D1的位置,此时C1D1恰好经过点C,则∠ABA1=______°.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】8筐白菜,以每25千克为标准,超过的千克数记作正数,不足的千克数记作负数,称后的纪录如下:

回答下列问题:
(1)这8筐白菜中最接近标准重量的这筐白菜重______ 千克;
(2)与标准重量比较,8筐白菜总计超过或不足多少千克?
(3)若白菜每千克售价2元,则出售这8筐白菜可卖多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购进一批单价为16元的日用品,销售一段时间后,为了获得更多利润,商店决定提高销售价格.经试验发现,若按每件20元的价格销售时,每月能卖360件;若按每件25元的价格销售时,每月能卖210件.假定每月销售件数y(件)是价格x(元/件)的一次函数.
(1)试求y与x之间的关系式;
(2)在商品不积压,且不考虑其它因素的条件下,问销售价格定为多少时,才能使每月获得最大利润?每月的最大利润是多少(总利润=总收入﹣总成本)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列变形中:
①由方程![]() =2去分母,得x﹣12=10;
=2去分母,得x﹣12=10;
②由方程![]() x=
x=![]() 两边同除以
两边同除以![]() ,得x=1;
,得x=1;
③由方程6x﹣4=x+4移项,得7x=0;
④由方程2﹣![]() 两边同乘以6,得12﹣x﹣5=3(x+3).
两边同乘以6,得12﹣x﹣5=3(x+3).
错误变形的个数是( )个.
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在解决数学问题的过程中,我们常用到“分类讨论”的数学思想,下面是运用分类讨论的数学思想解决问题的过程,请仔细阅读,并解答题目后提出的(探究).
(提出问题)两个有理数a、b满足a、b同号,求![]() 的值.
的值.
(解决问题)解:由a、b同号,可知a、b有两种可能:①当a,b都正数;②当a,b都是负数.①若a、b都是正数,即a>0,b>0,有|a|=a,|b|=b,则![]() =
=![]() =1+1=2;②若a、b都是负数,即a<0,b<0,有|a|=﹣a,|b|=﹣b,则
=1+1=2;②若a、b都是负数,即a<0,b<0,有|a|=﹣a,|b|=﹣b,则![]() =
=![]() =(﹣1)+(﹣1)=﹣2,所以
=(﹣1)+(﹣1)=﹣2,所以![]() 的值为2或﹣2.
的值为2或﹣2.
(探究)请根据上面的解题思路解答下面的问题:
(1)两个有理数a、b满足a、b异号,求![]() 的值;
的值;
(2)已知|a|=3,|b|=7,且a<b,求a+b的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com