
����Ŀ��ij�̵깺��һ������Ϊ16Ԫ������Ʒ������һ��ʱ���Ϊ�˻�ø��������̵����������ۼ۸����鷢�֣�����ÿ��20Ԫ�ļ۸�����ʱ��ÿ������360��������ÿ��25Ԫ�ļ۸�����ʱ��ÿ������210�����ٶ�ÿ�����ۼ���y�������Ǽ۸�x��Ԫ/������һ�κ�����
��1������y��x֮��Ĺ�ϵʽ��
��2������Ʒ����ѹ���Ҳ������������ص������£������ۼ۸�Ϊ����ʱ������ʹÿ�»���������ÿ�µ���������Ƕ��٣�������=�����멁�ܳɱ�����
���𰸡�
��1���⣺��������y=kx+b������
![]()
��� ![]()
��y=��30x+960��16��x��32��
��2���⣺ÿ�»������P=����30x+960����x��16��
=30����x+32����x��16��
=30����x2+48x��512��
=��30��x��24��2+1920
����16��x��32��Χ�ڣ���x=24ʱ��P�����ֵ�����ֵΪ1920��
�𣺵��۸�Ϊ24Ԫʱ������ʹÿ�»����������������Ϊ1920Ԫ
����������1���ȸ���������y=kx+b���ֱ�Ѷ�Ӧ��x=20��y=360��x=25��y=210�������ô���ϵ������⼴�ɣ���2�����ݡ�������=�����멁�ܳɱ����г�����ÿ�»������P��x֮��ĺ�����ϵʽ�������ó����κ���P=��30��x��24��2+1920���������ֵ���ɣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ������һ����Լӹ�![]() ��
��![]() ��������ӹ�
��������ӹ�![]() ��
��![]() �����ÿһ��
�����ÿһ��![]() ���������
���������![]() ���������װ��һ�������ij���乲��
���������װ��һ�������ij���乲��![]() �����ˣ���Ӧ��ΰ�����Щ���ˣ�ʹ�ӹ�����������պÿ������ף�
�����ˣ���Ӧ��ΰ�����Щ���ˣ�ʹ�ӹ�����������պÿ������ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͬһֱ������ϵ�У�һ�κ���y=ax+c�Ͷ��κ���y=ax2+c��ͼ�����Ϊ�� ��
A.
B.
C.
D.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
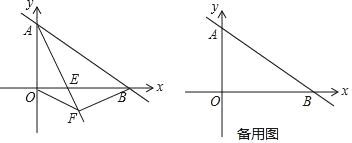
����Ŀ����ͼ����֪һ�κ���y=��![]() x+6��ͼ���������ύ��A��B���㣬AEƽ�֡�BAO����x���ڵ�E��
x+6��ͼ���������ύ��A��B���㣬AEƽ�֡�BAO����x���ڵ�E��
��1�����B�����꼰ֱ��AE�ı���ʽ��
��2������B��BF��AE������ΪF����y������һ��P��ʹ�߶�PE+PF��ֵ��С�����P�����ꣻ
��3��������֪������AEƽ�֡�BAO����x���ڵ�E���ı�Ϊ����E���߶�OB�ϵ�һ�����㣨��E�����O��B�غϣ���������B��BF��AE������ΪF����EFΪ����������EFMN������M������������ʱ����E�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O��ֱ������D��AB���ӳ����ϣ�BD=OB����C��Բ�ϣ���CAB=30�㣮 
��1����֤��DC�ǡ�O�����ߣ�
��2����BD=1cm����AC�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У���֪��A��3��4������OA������ԭ��O��ʱ����ת90����OA�䣬���A��������� �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ���ı���ABCD�У�AD��BC��AD=CD��E�ǶԽ���BD��һ�㣬��EA=EC��
��1����֤���ı���ABCD�����Σ�
��2�����BE=BC������CBE����BCE=2��3����֤���ı���ABCD�������Σ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ֽƬABCD�У��Խ���AC��BD���ڵ�O���۵�������ֽƬABCD��ʹAD����BD�ϣ���Aǡ����BD�ϵĵ�F�غ�.չ�����ۺ�DE�ֱ�AB��AC�ڵ�E��G.����GF.���н��ۣ��١�AGD=112.5�㣻��AD��AE=2����S��AGD=S��OGD�����ı���AEFG�����Σ���BE=2 OG��������ȷ���۵������______.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ᰴ��ͼ��ʾ�ӵ�A��ʼ�۳�һ�ȱ���ABC����A��ʾ����Ϊx��3�� B��ʾ����Ϊ2x��5��C��ʾ����Ϊ5��x����x=_______������ABC���ҹ��������2016���_____�غϣ�����A��B��C��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com