
【题目】如图,已知二次函数y=ax2+2x+c图象经过点A (1,4)和点C (0,3).
(1)求该二次函数的解析式;
(2)结合函数图象,直接回答下列问题:
①当﹣1<x<2时,求函数y的取值范围: .
②当y≥3时,求x的取值范围: .

【答案】(1)y=﹣x2+2x+3;(2)0<y≤4,0≤x≤2.
【解析】
(1)把A点和C点坐标代入y=ax2+2x+c得到二元一次方程组,然后解方程组求出a、c即可得到抛物线解析式;
(2)①先分别计算出x为-1和2时的函数值,然后根据二次函数的性质写出对应的函数值的范围;②先计算出函数值为3所对应的自变量的值,然后根据二次函数的性质写出y≥3时,x的取值范围.
(1)将点A和点C的坐标代入函数解析式,得![]() ,
,
解得![]() ,
,
二次函数的解析式为y=﹣x2+2x+3;
(2)由图象知,①当﹣1<x<2时,求函数y的取值范围:0<y≤4.
②当y≥3时,求x的取值范围:0≤x≤2.
故答案为:0<y≤4,0≤x≤2.


科目:初中数学 来源: 题型:
【题目】综合与探究:
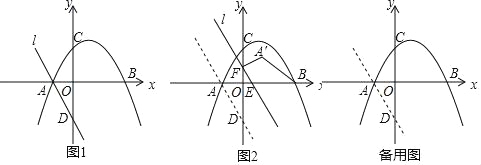
如图1,抛物线y=﹣![]() x2+
x2+![]() x+
x+![]() 与x轴分别交于A、B两点(点A在点B的左侧),与y轴交于C点.经过点A的直线l与y轴交于点D(0,﹣
与x轴分别交于A、B两点(点A在点B的左侧),与y轴交于C点.经过点A的直线l与y轴交于点D(0,﹣![]() ).
).
(1)求A、B两点的坐标及直线l的表达式;
(2)如图2,直线l从图中的位置出发,以每秒1个单位的速度沿x轴的正方向运动,运动中直线l与x轴交于点E,与y轴交于点F,点A 关于直线l的对称点为A′,连接FA′、BA′,设直线l的运动时间为t(t>0)秒.探究下列问题:
①请直接写出A′的坐标(用含字母t的式子表示);
②当点A′落在抛物线上时,求直线l的运动时间t的值,判断此时四边形A′BEF的形状,并说明理由;
(3)在(2)的条件下,探究:在直线l的运动过程中,坐标平面内是否存在点P,使得以P,A′,B,E为顶点的四边形为矩形?若存在,请直接写出点P的坐标; 若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把正方形铁片OABC置于平面直角坐标系中,顶点A的坐标为(3,0),点P(1,2)在正方形铁片上,将正方形铁片绕其右下角的顶点按顺时针方向依次旋转90°,第一次旋转至图①位置,第二次旋转至图②位置…,则正方形铁片连续旋转2017次后,点P的坐标为____________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知菱形ABCD的对角线相交于点O,延长AB至点E,使BE=AB,连接CE.

(1)求证:BD=EC;
(2)若∠E=50°,求∠BAO的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】重庆电视台组织了一次学生夏令营活动,有小学生、初中生、高中生和大学生参加,共200人,各类学生人数比例见扇形统计图.
(1)参加这次夏令营活动的初中生共有__________人.
(2)活动组织者号召参加这次夏令营活动的所有学生为贫困学生捐款. 结果小学生每人捐款5元,初中生每人捐款10元,高中生每人捐款15元,大学生每人捐款20元,把每个学生的捐款数(以元为单位)一一记录下来,则在这组数据中,中位数是 元,求出平均每人捐款多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,海中有一个小岛A,它的周围15海里内有暗礁,今有货船由西向东航行,开始在A岛南偏西60° 的B处,往东航行20海里后到达该岛南偏西30° 的C处后,货船继续向东航行,你认为货船航行途中_____ 触礁的危险.(填写:“有”或“没有”)
参考数据:sin60°=cos30°≈0.866.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高学生书写汉字的能力.增强保护汉字的意识,我区举办了“汉字听写大赛”,经选拔后有50名学生参加决赛,这50名学生同时听写50个汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
组别 | 成绩x分 | 频数(人数) |
第1组 | 25≤x<30 | 4 |
第2组 | 30≤x<35 | 6 |
第3组 | 35≤x<40 | 14 |
第4组 | 40≤x<45 | a |
第5组 | 45≤x<50 | 10 |
请结合图表完成下列各题:
(1)求表中a的值;
(2)请把频数分布直方图补充完整;
(3)若测试成绩不低于40分为优秀,则本次测试的优秀率是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 是等边三角形.
是等边三角形.
(1)将![]() 绕点
绕点![]() 逆时针旋转角
逆时针旋转角![]() (
(![]() );得到
);得到![]() ,
,![]() 和
和![]() 所在直线相交于点
所在直线相交于点![]() .
.
①如图![]() ,当
,当![]() 时,
时,![]() 与
与![]() 是否全等? (填“是”或“否”),
是否全等? (填“是”或“否”),![]() 度;
度;
②当![]() 旋转到如图
旋转到如图![]() 所在位置时,求
所在位置时,求![]() 的度数;
的度数;
(2)如图![]() ,在
,在![]() 和
和![]() 上分别截取点
上分别截取点![]() 和
和![]() ,使
,使![]() ,
,![]() ,连接
,连接![]() ,将
,将![]() 绕点
绕点![]() 逆时针旋转角(
逆时针旋转角(![]() ),得到
),得到![]() ,
,![]() 和
和![]() 所在直线相交于点
所在直线相交于点![]() ,请利用图
,请利用图![]() 探索
探索![]() 的度数,直接写出结果,不必说明理由.
的度数,直接写出结果,不必说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 经过
经过![]() 、
、![]() 、
、![]() 三点.
三点.
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 如图①,在抛物线的对称轴上是否存在点
如图①,在抛物线的对称轴上是否存在点![]() ,使得四边形
,使得四边形![]() 的周长最小?若存在,求出四边形
的周长最小?若存在,求出四边形![]() 周长的最小值;若不存在,请说明理由.
周长的最小值;若不存在,请说明理由.
![]() 如图②,点
如图②,点![]() 是线段
是线段![]() 上一动点,连接
上一动点,连接![]() ,在线段
,在线段![]() 上是否存在这样的点
上是否存在这样的点![]() ,使
,使![]() 为等腰三角形且
为等腰三角形且![]() 为直角三角形?若存在,求点
为直角三角形?若存在,求点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com