
【题目】重庆电视台组织了一次学生夏令营活动,有小学生、初中生、高中生和大学生参加,共200人,各类学生人数比例见扇形统计图.
(1)参加这次夏令营活动的初中生共有__________人.
(2)活动组织者号召参加这次夏令营活动的所有学生为贫困学生捐款. 结果小学生每人捐款5元,初中生每人捐款10元,高中生每人捐款15元,大学生每人捐款20元,把每个学生的捐款数(以元为单位)一一记录下来,则在这组数据中,中位数是 元,求出平均每人捐款多少元?

【答案】(1)80;(2)10;平均每人捐款11.5元.
【解析】
(1)参加这次夏令营活动的初中生所占比例是:110%20%30%=40%,就可以求出人数.
(2)小学生、高中生和大学生的人数为200×20%=40,200×30%=60,200×10%=20,根据平均数公式就可以求出平均数.
(3)因为初中生最多,所以众数为初中生捐款数.
(1)参加这次夏令营活动的初中生共有200×(110%20%30%)=80人;
故填:80;
(2)小学生、高中生和大学生的人数为200×20%=40,200×30%=60,200×10%=20,
∴小学生、初中生、高中生和大学生的人数分别为40,80,60,20,捐款金额依次为5,10,15,20
所以捐款数的100、101位在初中生中,即为10元.
故填:10;
平均每人捐款=![]() =11.5(元);
=11.5(元);
故平均每人捐款11.5元.


科目:初中数学 来源: 题型:
【题目】科技改变世界.2017年底,快递分拣机器人从微博火到了朋友圈,据介绍,这些机器人不仅可以自动规划最优路线,将包裹准确地放入相应的格口,还会感应避让障碍物,自动归队取包裹.没电的时候还会自己找充电桩充电.某快递公司启用80台A种机器人、300台B种机器人分拣快递包裹.A,B两种机器人全部投入工作,1小时共可以分拣1.44万件包裹,若全部A种机器人工作3小时,全部B种机器人工作2小时,一共可以分拣3.12万件包裹.
(1)求两种机器人每台每小时各分拣多少件包裹;
(2)为了进一步提高效率,快递公司计划再购进A,B两种机器人共200台,若要保证新购进的这批机器人每小时的总分拣量不少于7000件,求最多应购进A种机器人多少台?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点A、D在y轴正半轴上,点B、C分别在x轴上,CD平分∠ACB,与y轴交于D点,∠CAO=90°-∠BDO.
(1)求证:AC=BC:
(2)如图2,点C的坐标为(4,0),点E为AC上一点,且∠DEA=∠DBO,求BC+EC的长;

(3)如图3,过D作DF⊥AC于F点,点H为FC上一动点,点G为OC上一动点,当H在FC上移动、点G在OC上移动时,始终满足∠GDH=∠GDO+∠FDH,试判断FH、GH、OG这三者之间的数量关系,写出你的结论并加以证明.
 (图3)
(图3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E是对角线BD上一点,且满足BE=BC.连接CE并延长交AD于点F,连接AE,过B点作BG⊥AE于点G,延长BG交AD于点H.在下列结论中:
①AH=DF; ②∠AEF=45°; ③S四边形EFHG=S△DEF+S△AGH,
其中正确的结论有_____________________.(填正确的序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,如图所示的函数图象是由函数y=(x﹣1)2+1(x≥0)的图象C1和图象C2组成中心对称图形,对称中心为点(0,2).已知不重合的两点A、B分别在图象C1和C2上,点A、B的横坐标分别为a、b,且a+b=0.当b<x≤a时该函数的最大值和最小值均与a、b的值无关,则a的取值范围为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+2x+c图象经过点A (1,4)和点C (0,3).
(1)求该二次函数的解析式;
(2)结合函数图象,直接回答下列问题:
①当﹣1<x<2时,求函数y的取值范围: .
②当y≥3时,求x的取值范围: .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校把一块形状为直角三角形的废地开辟为生物园,如图所示,∠ACB=90°,AC=40m,BC=30m.线段CD是一条水渠,且D点在边AB上,已知水渠的造价为800元![]() ,问:当水渠的造价最低时,CD长为多少米?最低造价是多少元?
,问:当水渠的造价最低时,CD长为多少米?最低造价是多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】化工材料经销公司购进一种化工原料若干千克,价格为每千克30元。物价部门规定其销售单价不高于每千克60元,不低于每千克30元。经市场调查发现:日销售量y(千克)是销售单价x(元)的一次函数,且当x=60时,y=80;x=50时,y=100。在销售过程中,每天还要支付其他费用450元。
(1)求出y与x的函数关系式,并写出自变量x的取值范围。
(2)求该公司销售该原料日获利w(元)与销售单价x(元)之间的函数关系式。
(3)当销售单价为多少元时,该公司日获利最大?最大获利是多少元。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景:在![]() 中,
中,![]() 、
、![]() 、
、![]() 三边的长分别为
三边的长分别为![]() 、
、![]() 、
、![]() ,求这个三角形的面积.小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为
,求这个三角形的面积.小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为 ![]() ),在网格中画出格点
),在网格中画出格点 ![]() (即
(即 ![]() 三个顶点都在小正方形的顶点处),如图所示,这样借用网格就能计算出它的面积.
三个顶点都在小正方形的顶点处),如图所示,这样借用网格就能计算出它的面积.
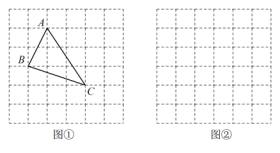
(1)请你直接写出 ![]() 的面积为 .
的面积为 .
(2)若![]() 三边的长分别为
三边的长分别为![]() 、
、![]() 、
、![]() 运用构图法求出这三角形的面积.
运用构图法求出这三角形的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com