
【题目】科技改变世界.2017年底,快递分拣机器人从微博火到了朋友圈,据介绍,这些机器人不仅可以自动规划最优路线,将包裹准确地放入相应的格口,还会感应避让障碍物,自动归队取包裹.没电的时候还会自己找充电桩充电.某快递公司启用80台A种机器人、300台B种机器人分拣快递包裹.A,B两种机器人全部投入工作,1小时共可以分拣1.44万件包裹,若全部A种机器人工作3小时,全部B种机器人工作2小时,一共可以分拣3.12万件包裹.
(1)求两种机器人每台每小时各分拣多少件包裹;
(2)为了进一步提高效率,快递公司计划再购进A,B两种机器人共200台,若要保证新购进的这批机器人每小时的总分拣量不少于7000件,求最多应购进A种机器人多少台?

【答案】(1)A种机器人每台每小时各分拣30件包裹,B种机器人每台每小时各分拣40件包裹(2)最多应购进A种机器人100台
【解析】
(1)A种机器人每台每小时各分拣x件包裹,B种机器人每台每小时各分拣y件包裹,根据题意列方程组即可得到结论;
(2)设最多应购进A种机器人a台,购进B种机器人(200a)台,由题意得,根据题意两不等式即可得到结论.
(1)A种机器人每台每小时各分拣x件包裹,B种机器人每台每小时各分拣y件包裹,
由题意得,![]() ,
,
解得,![]() ,
,
答:A种机器人每台每小时各分拣30件包裹,B种机器人每台每小时各分拣40件包裹;
(2)设最多应购进A种机器人a台,购进B种机器人(200﹣a)台,
由题意得,30a+40(200﹣a)≥7000,
解得:a≤100,则最多应购进A种机器人100台.


科目:初中数学 来源: 题型:
【题目】如图,在水上治安指挥塔![]() 西侧两条航线
西侧两条航线![]() 、
、![]() 上有两艘巡逻艇
上有两艘巡逻艇![]() 与
与![]() 所在航线靠近
所在航线靠近![]() ,直线
,直线![]() 、
、![]() 间的距离
间的距离![]() ,点
,点![]() 在点
在点![]() 的南偏西
的南偏西![]() 方向上,且
方向上,且![]() ,
,![]() 在
在![]() 的北偏东
的北偏东![]() 方向上.求:
方向上.求:

![]() 巡逻艇
巡逻艇![]() 与塔
与塔![]() 之间的距离
之间的距离![]() .(结果保留根号)
.(结果保留根号)
![]() 已知巡逻艇
已知巡逻艇![]() 的速度每小时比巡逻艇
的速度每小时比巡逻艇![]() 快
快![]() ,当两艘巡逻艇同时到达指挥塔
,当两艘巡逻艇同时到达指挥塔![]() 的正南方向时,求巡逻艇
的正南方向时,求巡逻艇![]() 的速度.
的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年黄金价格一路走高,![]() 月份的黄金价格比
月份的黄金价格比![]() 月份增长了
月份增长了![]() ,由于受国际金价的影响,预计
,由于受国际金价的影响,预计![]() 月份的黄金价格比
月份的黄金价格比![]() 月份增长
月份增长![]() ,若这两月黄金价格的平均增长率为
,若这两月黄金价格的平均增长率为![]() ,则
,则![]() 满足的关系式为( )
满足的关系式为( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车销售公司经销某品牌A款汽车,随着汽车的普及,其价格也在不断下降.今年5月份A款汽车的售价比去年同期每辆降价2万元.如果卖出相同数量的A款汽车,去年销售额为100万元,今年销售额只有90万元.
(1)今年5月份A款汽车每辆销售多少万元?
(2)为了增加收入,汽车销售公司决定再经销同品牌的B款汽车,已知A款汽车每辆进价为8.5万元,B款汽车每辆进价为6万元,公司预计用多于100万元且少于110万元的资金购进这两款汽车共15辆,问有几种进货方案?
(3)在(2)的前提下,如果B款汽车每辆售价为12万元,为打开B款汽车的销路,公司决定每售出一辆B款汽车,奖励顾客现金1.8万元,怎样进货公司的利润最大(假设能全部卖出)?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,C,E,G四点在同一直线上,分别以线段AC,CE,EG为边在AG同侧作等边三角形△ABC,△CDE,△EFG,连接AF,分别交BC,DC,DE于点H,I,J,若AC=1,CE=2,EG=3,则△DIJ的面积是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
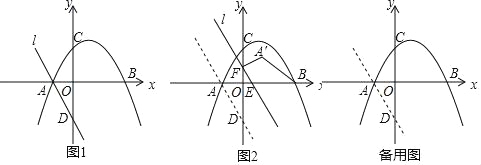
【题目】综合与探究:
如图1,抛物线y=﹣![]() x2+
x2+![]() x+
x+![]() 与x轴分别交于A、B两点(点A在点B的左侧),与y轴交于C点.经过点A的直线l与y轴交于点D(0,﹣
与x轴分别交于A、B两点(点A在点B的左侧),与y轴交于C点.经过点A的直线l与y轴交于点D(0,﹣![]() ).
).
(1)求A、B两点的坐标及直线l的表达式;
(2)如图2,直线l从图中的位置出发,以每秒1个单位的速度沿x轴的正方向运动,运动中直线l与x轴交于点E,与y轴交于点F,点A 关于直线l的对称点为A′,连接FA′、BA′,设直线l的运动时间为t(t>0)秒.探究下列问题:
①请直接写出A′的坐标(用含字母t的式子表示);
②当点A′落在抛物线上时,求直线l的运动时间t的值,判断此时四边形A′BEF的形状,并说明理由;
(3)在(2)的条件下,探究:在直线l的运动过程中,坐标平面内是否存在点P,使得以P,A′,B,E为顶点的四边形为矩形?若存在,请直接写出点P的坐标; 若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
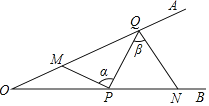
【题目】如图,∠AOB=20°,点M,N分别是边OA,OB上的定点,点P,Q分别是边OB、OA上的动点,记∠MPQ=α,∠PQN=β,当MP+PQ+QN最小时,则β﹣α的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】重庆电视台组织了一次学生夏令营活动,有小学生、初中生、高中生和大学生参加,共200人,各类学生人数比例见扇形统计图.
(1)参加这次夏令营活动的初中生共有__________人.
(2)活动组织者号召参加这次夏令营活动的所有学生为贫困学生捐款. 结果小学生每人捐款5元,初中生每人捐款10元,高中生每人捐款15元,大学生每人捐款20元,把每个学生的捐款数(以元为单位)一一记录下来,则在这组数据中,中位数是 元,求出平均每人捐款多少元?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com