
【题目】如图,A,C,E,G四点在同一直线上,分别以线段AC,CE,EG为边在AG同侧作等边三角形△ABC,△CDE,△EFG,连接AF,分别交BC,DC,DE于点H,I,J,若AC=1,CE=2,EG=3,则△DIJ的面积是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】
根据等边三角形的性质得到FG=EG=3,∠AGF=∠FEG=60°,根据三角形的内角和得到∠AFG=90°,根据相似三角形的性质得到![]() =
=![]() =
=![]() ,
,![]() =
=![]() =
=![]() ,根据三角形的面积公式即可得到结论.
,根据三角形的面积公式即可得到结论.
∵AC=1,CE=2,EG=3,
∴AG=6,
∵△EFG是等边三角形,
∴FG=EG=3,∠AGF=∠FEG=60°,
∵AE=EF=3,
∴∠FAG=∠AFE=30°,
∴∠AFG=90°,
∵△CDE是等边三角形,
∴∠DEC=60°,
∴∠AJE=90°,JE∥FG,
∴△AJE∽△AFG,
∴![]() =
=![]() =
=![]() ,
,
∴EJ=![]() ,
,
∵∠BCA=∠DCE=∠FEG=60°,
∴∠BCD=∠DEF=60°,
∴∠ACI=∠AEF=120°,
∵∠IAC=∠FAE,
∴△ACI∽△AEF,
∴![]() =
=![]() =
=![]() ,
,
∴CI=1,DI=1,DJ=![]() ,
,
∴IJ=![]() ,
,
∴![]() =
=![]() DIIJ=
DIIJ=![]() ×
×![]() ×
×![]() .
.
故选:A.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,∠AOB=90°,OA=12cm,OB=8cm,一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O,机器人立即从点B出发,沿BC方向匀速前进拦截小球,恰好在点C处截住了小球.如果小球滚动的速度与机器人行走的速度相等,并且它们的运动时间也相等.
(1)请用直尺和圆规作出C处的位置,不必叙述作图过程,保留作图痕迹;
(2)求线段OC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作图题(不写作法)已知:如图,在平面直角坐标系中.
(1)作出△ABC关于y轴对称的△A1B1C1,并写出△A1B1C1三个顶点的坐标;
(2)求△ABC的面积;
(3)在x轴上画点P,使PA+PC最小.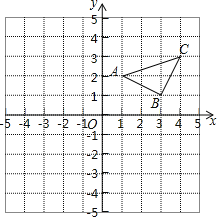
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 和
和![]() 是两个边长都为
是两个边长都为![]() 的等边三角形,且点
的等边三角形,且点![]() ,
,![]() ,
,![]() ,
,![]() 在同一直线上,连接
在同一直线上,连接![]() ,
,![]() .
.
![]() 求证:四边形
求证:四边形![]() 是平行四边形;
是平行四边形;
![]() 若
若![]() 沿着
沿着![]() 的方向匀速运动,
的方向匀速运动,![]() 不动,当
不动,当![]() 运动到点
运动到点![]() 与点
与点![]() 重合时,四边形
重合时,四边形![]() 是什么特殊的四边形?说明理由.
是什么特殊的四边形?说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】科技改变世界.2017年底,快递分拣机器人从微博火到了朋友圈,据介绍,这些机器人不仅可以自动规划最优路线,将包裹准确地放入相应的格口,还会感应避让障碍物,自动归队取包裹.没电的时候还会自己找充电桩充电.某快递公司启用80台A种机器人、300台B种机器人分拣快递包裹.A,B两种机器人全部投入工作,1小时共可以分拣1.44万件包裹,若全部A种机器人工作3小时,全部B种机器人工作2小时,一共可以分拣3.12万件包裹.
(1)求两种机器人每台每小时各分拣多少件包裹;
(2)为了进一步提高效率,快递公司计划再购进A,B两种机器人共200台,若要保证新购进的这批机器人每小时的总分拣量不少于7000件,求最多应购进A种机器人多少台?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,动点P从点B出发,沿BC,CD,DA运动至点A停止.设点P运动的路程为x,△ABP的面积为y,如果y关于x的函数图象如图2所示.
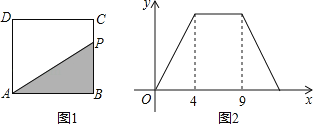
(1)求△ABC的面积;
(2)求y关于x的函数解析式;
(3)当△ABP的面积为5时,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请阅读下列材料:
问题:如图1,在等边三角形ABC内有一点P,且PA=2,PB=![]() ,PC=1、求∠BPC度数的大小和等边三角形ABC的边长.
,PC=1、求∠BPC度数的大小和等边三角形ABC的边长.
李明同学的思路是:将△BPC绕点B逆时针旋转60°,画出旋转后的图形(如图2),连接PP′,可得△P′PB是等边三角形,而△PP′A又是直角三角形(由勾股定理的逆定理可证),所以∠AP′B=150°,而∠BPC=∠AP′B=150°,进而求出等边△ABC的边长为![]() ,问题得到解决.
,问题得到解决.
请你参考李明同学的思路,探究并解决下列问题:如图3,在正方形ABCD内有一点P,且PA=![]() ,BP=
,BP=![]() ,PC=1.求∠BPC度数的大小和正方形ABCD的边长.
,PC=1.求∠BPC度数的大小和正方形ABCD的边长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,如图所示的函数图象是由函数y=(x﹣1)2+1(x≥0)的图象C1和图象C2组成中心对称图形,对称中心为点(0,2).已知不重合的两点A、B分别在图象C1和C2上,点A、B的横坐标分别为a、b,且a+b=0.当b<x≤a时该函数的最大值和最小值均与a、b的值无关,则a的取值范围为_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com