
【题目】请阅读下列材料:
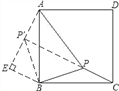
问题:如图1,在等边三角形ABC内有一点P,且PA=2,PB=![]() ,PC=1、求∠BPC度数的大小和等边三角形ABC的边长.
,PC=1、求∠BPC度数的大小和等边三角形ABC的边长.
李明同学的思路是:将△BPC绕点B逆时针旋转60°,画出旋转后的图形(如图2),连接PP′,可得△P′PB是等边三角形,而△PP′A又是直角三角形(由勾股定理的逆定理可证),所以∠AP′B=150°,而∠BPC=∠AP′B=150°,进而求出等边△ABC的边长为![]() ,问题得到解决.
,问题得到解决.
请你参考李明同学的思路,探究并解决下列问题:如图3,在正方形ABCD内有一点P,且PA=![]() ,BP=
,BP=![]() ,PC=1.求∠BPC度数的大小和正方形ABCD的边长.
,PC=1.求∠BPC度数的大小和正方形ABCD的边长.

【答案】(1)135°;(2)![]() ;
;
【解析】试题分析:
(1)如图,将△BPC绕点B逆时针旋转90°,得△BP′A,则△BPC≌△BP′A,由此可得:AP′=PC=1,BP=BP′=![]() ;连接PP′,由∠PBP′=90°可得PP′=2,∠BP′P=45°,这样在△AP′P中由勾股定理的逆定理可得∠AP′P=90°,从而可得∠AP′B=135°,由此可得∠BPC=∠AP′B=135°;
;连接PP′,由∠PBP′=90°可得PP′=2,∠BP′P=45°,这样在△AP′P中由勾股定理的逆定理可得∠AP′P=90°,从而可得∠AP′B=135°,由此可得∠BPC=∠AP′B=135°;
(2)过点B作BE⊥AP′,交AP′的延长线于点E,结合(1)中∠AP′B=135°可证得△BEP′是等腰直角三角形,结合BP′=![]() ,可得EP′=BE=1,从而可得AE=2,结合BE=1在Rt△ABE中由勾股定理即可求得AB的长.
,可得EP′=BE=1,从而可得AE=2,结合BE=1在Rt△ABE中由勾股定理即可求得AB的长.
试题解析:
(1)如图,
将△BPC绕点B逆时针旋转90°,得△BP′A,则△BPC≌△BP′A.
∴AP′=PC=1,BP=BP′=![]() ;
;
连接PP′,
在Rt△BP′P中,
∵BP=BP′=![]() ,∠PBP′=90°,
,∠PBP′=90°,
∴PP′=2,∠BP′P=45°;
在△AP′P中,AP′=1,PP′=2,AP=![]() ,
,
∵![]() ,即AP′2+PP′2=AP2;
,即AP′2+PP′2=AP2;
∴△AP′P是直角三角形,即∠AP′P=90°,
∴∠AP′B=135°,
∴∠BPC=∠AP′B=135°.
(2)过点B作BE⊥AP′,交AP′的延长线于点E,
∴∠BEP′=90°,
∵∠AP′B=135°,
∴∠EP′B=45°,
∴△BEP′是等腰直角三角形,
∵BP′=![]() ,
,
∴EP′=BE=1,
∴AE=AP′+EP′=2;
∴在Rt△ABE中,由勾股定理,得AB=![]() ;
;
∴∠BPC=135°,正方形边长为![]() .
.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案科目:初中数学 来源: 题型:
【题目】最近,“校园安全”受到全社会的广泛关注,巫溪中学对部分学生就校园安全知识的了解程度, 采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了如下两幅尚不完整的统计图,请你根据统计图中所提供的信息解答下列问题:
(1)扇形统计图中“基本了解”部分对应扇形的圆心角为 度;请补全条形统计图;
(2)若达到“了解”程度的人中有1名男生,2名女生,达到“不了解”程度的人中有1名男生和1名女生,若分别从达到“了解”程度和“不了解”程度的人中分别抽取1人参加校园知识竞赛,请用树状图或列表法求出恰好抽到1名男生和1名女生的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,C,E,G四点在同一直线上,分别以线段AC,CE,EG为边在AG同侧作等边三角形△ABC,△CDE,△EFG,连接AF,分别交BC,DC,DE于点H,I,J,若AC=1,CE=2,EG=3,则△DIJ的面积是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
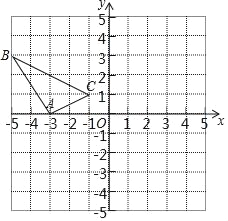
【题目】在边长为1个单位长度的小正方形组成的网格中,建立如图所示的平面直角坐标系△ABC是格点三角形(顶点在网格线的交点上)
(1)先作△ABC关于原点O成中心对称的△A1B1C1,再把△A1B1C1向上平移4个单位长度得到△A2B2C2;
(2)△A2B2C2与△ABC是否关于某点成中心对称?若是,直接写出对称中心的坐标;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
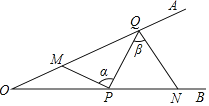
【题目】如图,∠AOB=20°,点M,N分别是边OA,OB上的定点,点P,Q分别是边OB、OA上的动点,记∠MPQ=α,∠PQN=β,当MP+PQ+QN最小时,则β﹣α的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
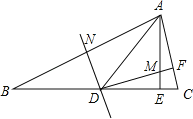
【题目】如图,在△ABC中,AE⊥BC于点E,∠B=22.5°,AB的垂直平分线DN交BC于点D,交AB于点N,DF⊥AC于点F,交AE于点M.求证:
(1)AE=DE;
(2)EM=EC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,将△ABC沿∠B的平分线折叠,使点A落在BC边上的点D处,设折痕交AC边于点E,继续沿直线DE折叠,若折叠后,BE与线段DC相交,且交点不与点C重合,则∠BAC的度数应满足的条件是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个暗箱中装有红、黄、白三种颜色的乒乓球(除颜色外其余均相同).其中白球、黄球各1个,若从中任意摸出一个球是白球的概率是![]() .
.
(1)求暗箱中红球的个数.
(2)先从暗箱中任意摸出一个球记下颜色后放回,再从暗箱中任意摸出一个球,求两次摸到的球颜色不同的概率(用树形图或列表法求解).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com