
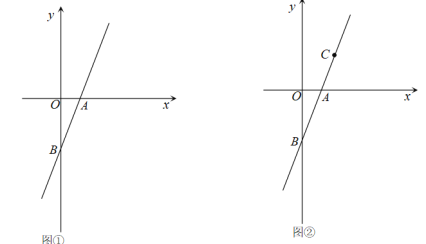
【题目】已知,直线y=2x-2与x轴交于点A,与y轴交于点B.
(1)如图①,点A的坐标为_______,点B的坐标为_______;
(2)如图②,点C是直线AB上不同于点B的点,且CA=AB.
①求点C的坐标;
②过动点P(m,0)且垂直与x轴的直线与直线AB交于点E,若点E不在线段BC上,则m的取值范围是_______;
(3)若∠ABN=45,求直线BN的解析式.
【答案】(1)(1,0),(0,-2);(2)C(2,2);m<0或m>2;(3)![]() 或y=-3x-2.
或y=-3x-2.
【解析】
(1)利用函数解析式和坐标轴上点的坐标特征即可解决问题;
(2)①如图②,过点C 作CD⊥x 轴,垂足是D.构造全等三角形,利用全等三角形的性质求得点C的坐标;
②由①可知D(2,0),观察图②,可知m的取值范围是:m<0或m>2;
(3)如图③中,作AN⊥AB,使得AN=AB,作NH⊥x轴于H,则△ABN是等腰直角三角形,∠ABN=45°.利用全等三角形的性质求出点N坐标,当直线BN′⊥直线BN时,直线BN′也满足条件,求出直线BN′的解析式即可.
解:(1)如图①,

令y=0,则2x-2=0,即x=1.所以A(1,0).
令x=0,则y=-2,即B(0,-2).
故答案是:(1,0);(0,-2);
(2)①如图②,

过点C 作CD⊥x 轴,垂足是D,
∵∠BOA=∠ADC=90°,
∠BAO=∠CAD,
CA=AB,
∴△BOA≌△CAD(AAS),
∴CD=OB=2,AD=OA=1,
∴C(2,2);
②由①可知D(2,0),观察图②,可知m的取值范围是:m<0或m>2.
故答案是:m<0或m>2;
(3)如图③,作AN⊥AB,使得AN=AB,作NH⊥x轴于H,则△ABN是等腰直角三角形,∠ABN=45°.

∵∠AOB=∠BAN=∠AHN=90°,
∴∠OAB+∠ABO=90°,∠OAB+∠HAN=90°,
∴∠ABO=∠HAN,
∵AB=AN,
∴△ABO≌△NAH(AAS),
∴AH=OB=2,NH=OA=1,
∴N(3,-1),
设直线BN的解析式为y=kx+b,
则有:![]() ,
,
解得 ,
,
∴直线BN的解析式为y=![]() x-2,
x-2,
当直线BN′⊥直线BN时,直线BN′也满足条件,直线BN′的解析式为:
![]() .
.
∴满足条件的直线BN的解析式为y=![]() x-2或y=-3x-2.
x-2或y=-3x-2.


科目:初中数学 来源: 题型:
【题目】如图,在四边形纸片ABCD中,∠B=∠D=90°,点E,F分别在边BC,CD上,将AB,AD分别沿AE,AF折叠,点B,D恰好都和点G重合,∠EAF=45°.
(1)求证:四边形ABCD是正方形;
(2)求证:三角形ECF的周长是四边形ABCD周长的一半;
(3)若EC=FC=1,求AB的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)若多项式2x3﹣8x2y+x+1与多项式﹣3x3﹣2mx2y+6x﹣9的差的值与字母y的取值无关,求m的值.
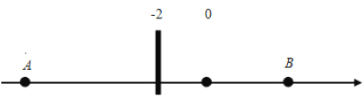
(2)已知有理数a,b,c在数轴上对应位置如图所示,化简:|a+b|﹣|b+c|+|a+c|.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在数轴上![]() 点表示数
点表示数![]() ,
,![]() 点表示数6,
点表示数6,
(1)A、B两点之间的距离等于_________;
(2)在数轴上有一个动点![]() ,它表示的数是
,它表示的数是![]() ,则
,则![]() 的最小值是_________;
的最小值是_________;
(3)若点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() ,点
,点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() ,请在数轴上找一点
,请在数轴上找一点![]() ,使
,使![]() ,则
,则![]() 点表示的数是_________;
点表示的数是_________;
(4)若在原点![]() 的左边2个单位处放一挡板,一小球甲从点
的左边2个单位处放一挡板,一小球甲从点![]() 处以5个单位/秒的速度向右运动;同时另一小球乙从点
处以5个单位/秒的速度向右运动;同时另一小球乙从点![]() 处以2个单位/秒的速度向左运动,在碰到挡板后(忽略球的大小,可看作一点)两球分别以原来的速度向相反的方向运动,设运动时间为
处以2个单位/秒的速度向左运动,在碰到挡板后(忽略球的大小,可看作一点)两球分别以原来的速度向相反的方向运动,设运动时间为![]() 秒,请用
秒,请用![]() 来表示甲、乙两小球之间的距离
来表示甲、乙两小球之间的距离![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明是个爱动脑筋的同学,在发现教材中的用方框在月历中移动的规律后,突发奇想,将连续的偶数2,4,6,8,…,排成如图:并用一个十字形框架框住其中的五个数,请你仔细观察十字形框架中的数字的规律,并回答下列问题:
(1)十字框中的五个数的和与中间的数16有什么关系?
(2)设中间的数为x,用代数式表示十字框中的五个数的和;
(3)若将十字框上下左右移动,可框住另外的五位数,其它五位数的和能等于2015吗?如能,写出这五位数,如不能,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小王同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了50户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图).
月均用水量(单位:t) | 频数 | 百分比 |
2≤x<3 | 2 | 4% |
3≤x<4 | 12 | 24% |
4≤x<5 |
|
|
5≤x<6 | 10 | 20% |
6≤x<7 |
| 12% |
7≤x<8 | 3 | 6% |
8≤x<9 | 2 | 4% |
(1)请根据题中已有的信息补全频数分布表和频数分布直方图;
(2)如果家庭月均用水量“大于或等于4t且小于7t”为中等用水量家庭,请你估计总体小王所居住的小区中等用水量家庭大约有多少户?
(3)从月均用水量在2≤x<3,8≤x<9这两个范围内的样本家庭中任意抽取2个,请用列举法(画树状图或列表)求抽取出的2个家庭来自不同范围的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形OABC的边OA,OC在坐标轴上,点B的坐标为(-4,4).点P从点A出发,以每秒1个单位长度的速度沿x轴向点O运动;点Q从点O同时出发,以相同的速度沿x轴的正方向运动,规定点P到达点O时,点Q也停止运动.连接BP,过P点作BP的垂线,与过点Q平行于y轴的直线l相交于点D.BD与y轴交于点E,连接PE.设点P运动的时间为t(s).

(1)写出∠PBD的度数和点D的坐标(点D的坐标用t表示);
(2)探索△POE周长是否随时间t的变化而变化,若变化,说明理由;若不变,试求这个定值.
(3)当t为何值时,△PBE为等腰三角形?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com