
【题目】如图:在数轴上![]() 点表示数
点表示数![]() ,
,![]() 点表示数6,
点表示数6,
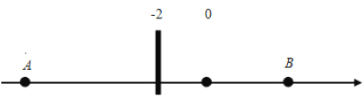
(1)A、B两点之间的距离等于_________;
(2)在数轴上有一个动点![]() ,它表示的数是
,它表示的数是![]() ,则
,则![]() 的最小值是_________;
的最小值是_________;
(3)若点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() ,点
,点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() ,请在数轴上找一点
,请在数轴上找一点![]() ,使
,使![]() ,则
,则![]() 点表示的数是_________;
点表示的数是_________;
(4)若在原点![]() 的左边2个单位处放一挡板,一小球甲从点
的左边2个单位处放一挡板,一小球甲从点![]() 处以5个单位/秒的速度向右运动;同时另一小球乙从点
处以5个单位/秒的速度向右运动;同时另一小球乙从点![]() 处以2个单位/秒的速度向左运动,在碰到挡板后(忽略球的大小,可看作一点)两球分别以原来的速度向相反的方向运动,设运动时间为
处以2个单位/秒的速度向左运动,在碰到挡板后(忽略球的大小,可看作一点)两球分别以原来的速度向相反的方向运动,设运动时间为![]() 秒,请用
秒,请用![]() 来表示甲、乙两小球之间的距离
来表示甲、乙两小球之间的距离![]() .
.
【答案】(1)16 (2)16 (3)2或14 (4)甲、乙两小球之间的距离![]() 为:
为:![]() 或
或![]() ,或
,或![]() .
.
【解析】
(1)根据数轴上两点之间的距离公式计算即可;
(2)先根据P点在数轴上的位置分类讨论,然后求最小值即可;
(3)由题意可知:点C距离B点较近,设点C所表示的数为y,然后根据点C与点B的位置分类讨论即可;
(4)根据题意:点A到表示﹣2的点的距离为:﹣2-(﹣10)=8,点B到表示﹣2的点的距离为:6-(﹣2)=8,甲球从A到﹣2所需时间为:8÷5=![]() s,乙球从B到﹣2所需时间为:8÷2=4s,然后用t分别表示出甲球从点A到表示﹣2的点之前和之后,甲球所表示的数,乙球从点B到表示﹣2的点之前和之后,乙球所表示的数,根据数轴上两点之间的距离公式,即可求出甲乙两球的距离.
s,乙球从B到﹣2所需时间为:8÷2=4s,然后用t分别表示出甲球从点A到表示﹣2的点之前和之后,甲球所表示的数,乙球从点B到表示﹣2的点之前和之后,乙球所表示的数,根据数轴上两点之间的距离公式,即可求出甲乙两球的距离.
解:(1)![]()
故答案为:16;
(2)根据数轴上两点的距离公式可知:![]() 表示点P与点A之间的距离,
表示点P与点A之间的距离,![]() 表示点P与点B之间的距离
表示点P与点B之间的距离
①若点P在A点左侧时,即x<﹣10,由下图可知:PB>AB=16,即![]()
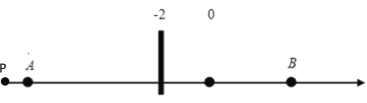
∴此时![]() ;
;
②若点P在线段AB上时,即﹣10≤x≤6,由下图可知:PA+PB=AB=16,
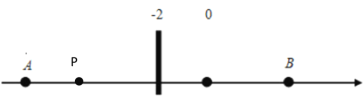
∴此时![]() ;
;
③若点P在B点右侧时,即x>6,由下图可知:PA>AB=16,即![]()
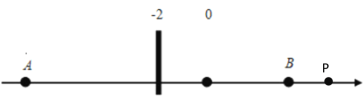
∴此时![]() ;
;
综上所述:![]() (当点P在线段AB上时,即﹣10≤x≤6,取等号)
(当点P在线段AB上时,即﹣10≤x≤6,取等号)
∴![]() 的最小值是16;
的最小值是16;
故答案为:16.
(3)∵![]()
∴点C距离B点较近
设点C所表示的数为y
①当C在B点左侧时,如下图所示,
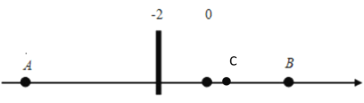
∴AC=y-(﹣10)=y+10,BC=6-y
∵![]()
∴y+10=3(6-y)
解得:y=2;
②当C在B点右侧时,如下图所示,
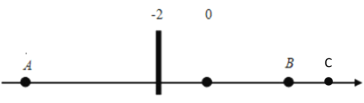
∴AC=y-(﹣10)=y+10,BC= y -6
∵![]()
∴y+10=3(y -6)
解得:y=14.
综上所述:![]() 点表示的数是2或14.
点表示的数是2或14.
(4)点A到表示﹣2的点的距离为:﹣2-(﹣10)=8,点B到表示﹣2的点的距离为:6-(﹣2)=8,甲球从A到﹣2所需时间为:8÷5=![]() s,乙球从B到﹣2所需时间为:8÷2=4s,
s,乙球从B到﹣2所需时间为:8÷2=4s,
∴运动![]() 秒钟后,甲球表示的数是:
秒钟后,甲球表示的数是:![]() 或
或![]() ;
;
乙球表示的数是:![]() 或
或![]() ,
,
∴![]() 或
或![]() ,或
,或![]() .
.
∴甲、乙两小球之间的距离![]() 为:
为:![]() 或
或![]() ,或
,或![]() .
.


科目:初中数学 来源: 题型:
【题目】已知点A在数轴上对应的数是a,点B在数轴上对应的数是b,且|a+4|+(b﹣1)2=0,现将A、B之间的距离记作|AB|,定义|AB|=|a﹣b|.
(1)求2019b+a的值;
(2)求|AB|的值;
(3)设点P在数轴上对应的数是x,当|PA|﹣|PB|=2时,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】改革开放40年以来,城乡居民生活水平持续快速提升,居民教育、文化和娱乐消费支出持续增长,已经成为居民各项消费支出中仅次于居住、食品烟酒、交通通信后的第四大消费支出,如图为北京市统计局发布的2017年和2018年我市居民人均教育、文化和娱乐消费支出的折线图.
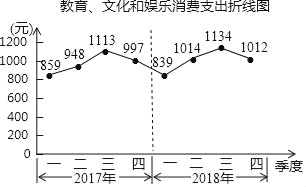
说明:在统计学中,同比是指本期统计数据与上一年同期统计数据相比较,例如2018年第二季度与2017年第二季度相比较;环比是指本期统计数据与上期统计数据相比较,例如2018年第二季度与2018年第一季度相比较.
根据上述信息,下列结论中错误的是( )
A. 2017年第二季度环比有所提高
B. 2017年第三季度环比有所提高
C. 2018年第一季度同比有所提高
D. 2018年第四季度同比有所提高
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,⊙O与AC相交于点D,∠BAC=45°,AB=BC.
(1)求证:BC是⊙O的切线;
(2)若⊙O的半径为2cm,求图中阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用火柴按下图中的方式搭图形:

(1)按图示规律补全表格:
图形编号 | ① | ② | ③ | ④ | ⑤ |
火柴棒根数 | 7 | 12 |
|
|
|
(2)按照这种方式搭下去,请写出搭第n个图形需要的火柴根数;
(3)小明发现:按照这种方式搭图形会产生若干个正方形,若使用187根火柴搭图形,图中会产生多少个正方形?
查看答案和解析>>
科目:初中数学 来源: 题型:
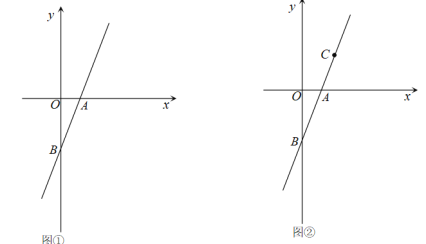
【题目】已知,直线y=2x-2与x轴交于点A,与y轴交于点B.
(1)如图①,点A的坐标为_______,点B的坐标为_______;
(2)如图②,点C是直线AB上不同于点B的点,且CA=AB.
①求点C的坐标;
②过动点P(m,0)且垂直与x轴的直线与直线AB交于点E,若点E不在线段BC上,则m的取值范围是_______;
(3)若∠ABN=45,求直线BN的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,以AC为直径作⊙O,交AB于D,过点O作OE∥AB,交BC于E.
(1)求证:ED为⊙O的切线;
(2)如果⊙O的半径为![]() ,ED=2,延长EO交⊙O于F,连接DF、AF,求△ADF的面积.
,ED=2,延长EO交⊙O于F,连接DF、AF,求△ADF的面积.

【答案】(1)证明见解析;(2)![]()
【解析】试题分析:(1)首先连接OD,由OE∥AB,根据平行线与等腰三角形的性质,易证得![]() ≌
≌![]() 即可得
即可得![]() ,则可证得
,则可证得![]() 为
为![]() 的切线;
的切线;
(2)连接CD,根据直径所对的圆周角是直角,即可得![]() 利用勾股定理即可求得
利用勾股定理即可求得![]() 的长,又由OE∥AB,证得
的长,又由OE∥AB,证得![]() 根据相似三角形的对应边成比例,即可求得
根据相似三角形的对应边成比例,即可求得![]() 的长,然后利用三角函数的知识,求得
的长,然后利用三角函数的知识,求得![]() 与
与![]() 的长,然后利用S△ADF=S梯形ABEF-S梯形DBEF求得答案.
的长,然后利用S△ADF=S梯形ABEF-S梯形DBEF求得答案.
试题解析:(1)证明:连接OD,

∵OE∥AB,
∴∠COE=∠CAD,∠EOD=∠ODA,
∵OA=OD,
∴∠OAD=∠ODA,
∴∠COE=∠DOE,
在△COE和△DOE中,
 ∴△COE≌△DOE(SAS),
∴△COE≌△DOE(SAS),
![]()
∴ED⊥OD,
∴ED是![]() 的切线;
的切线;
(2)连接CD,交OE于M,
在Rt△ODE中,
∵OD=32,DE=2,
![]()
∵OE∥AB,
∴△COE∽△CAB,
![]() ∴AB=5,
∴AB=5,
∵AC是直径,
![]()
![]()
![]()
![]()
∵EF∥AB,
![]()
![]()
![]()
∴S△ADF=S梯形ABEFS梯形DBEF
![]()
∴△ADF的面积为![]()

【题型】解答题
【结束】
25
【题目】【题目】已知,抛物线y=ax2+ax+b(a≠0)与直线y=2x+m有一个公共点M(1,0),且a<b.
(1)求b与a的关系式和抛物线的顶点D坐标(用a的代数式表示);
(2)直线与抛物线的另外一个交点记为N,求△DMN的面积与a的关系式;
(3)a=﹣1时,直线y=﹣2x与抛物线在第二象限交于点G,点G、H关于原点对称,现将线段GH沿y轴向上平移t个单位(t>0),若线段GH与抛物线有两个不同的公共点,试求t的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种水果的价格如表:
购买的质量(千克) | 不超过10千克 | 超过10千克 |
每千克价格 | 6元 | 5元 |
张欣两次共购买了25千克这种水果(第二次多于第一次),共付款132元.问张欣第一次、第二次分别购买了多少千克这种水果?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,CE![]() AD于点E,且CB=CE,点F为CD边上的一点,CB=CF,连接BF交CE于点G.
AD于点E,且CB=CE,点F为CD边上的一点,CB=CF,连接BF交CE于点G.
(1)若![]() ,CF=
,CF=![]() ,求CG的长;
,求CG的长;
(2)求证:AB=ED+CG

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com