
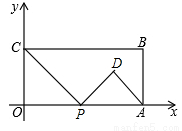
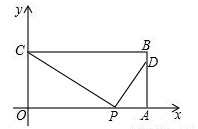
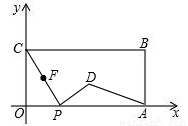
(本题14分)如图,在平面直角坐标系中,矩形OABC的两边OA、OC分别在x轴、y轴的正半轴上,OA=4,OC=2.点P从点O出发,沿x轴以每秒1个单位长的速度向点A匀速运动,当点P到达点A时停止运动,设点P运动的时间是t秒.将线段CP的中点绕点P按顺时针方向旋转90°得点D,点D随点P的运动而运动,连接DP、DA.
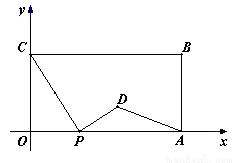
(1)请用含t的代数式表示出点D的坐标;
(2)求t为何值时,△DPA的面积最大,最大为多少?
(3)在点P从O向A运动的过程中,△DPA能否成为直角三角形?若能,求t的值.若不能,请说明理由;
(4)请直接写出随着点P的运动,点D运动路线的长.
(1)D(t+1,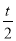 );(2)当t=2时,S最大=1;(3)能,2或3;(4)
);(2)当t=2时,S最大=1;(3)能,2或3;(4)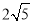 .
.
【解析】
试题分析:(1)设出P点坐标,再求出CP的中点坐标,根据相似的性质即可求出D点坐标;
(2)根据D点的坐标及三角形的面积公式直接求解即可;
(3)先判断出可能为直角的角,再根据勾股定理求解;
(4)根据点D的运动路线与OB平行且相等解答即可.
试题解析:(1)∵点P从点O出发,沿x轴以每秒1个单位长的速度向点A匀速运动,∴OP=t,而OC=2,∴P(t,0),设CP的中点为F,则F点的坐标为(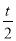 ,1),
,1),
∴将线段CP的中点F绕点P按顺时针方向旋转90°得点D,其坐标为(t+1,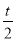 );
);
(2)∵D点坐标为(t+1,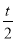 ),OA=4,∴S△DPA=
),OA=4,∴S△DPA=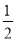 AP×
AP×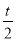 =
=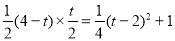 ,
,
∴当t=2时,S最大=1;
(3)能构成直角三角形.
①当∠PDA=90°时,PC∥AD,由勾股定理得,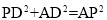 ,
,
即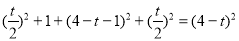 ,解得,t=2或t=-6(舍去).∴t=2秒.
,解得,t=2或t=-6(舍去).∴t=2秒.
②当∠PAD=90°时,此时点D在AB上,可知,△COP∽△PAD,
∴CP:PD=CO:PA,∴2:1=2:PA,PA=1,即t+1=4,t=3秒.
综上,可知当t为2秒或3秒时,△DPA能成为直角三角形.
(4)∵根据点D的运动路线与OB平行且相等,OB=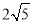 ,
,
∴点D运动路线的长为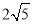 .
.
考点:1.二次函数的最值;2.待定系数法求一次函数解析式;3.直角三角形的性质;4.矩形的性质.


 名师点拨卷系列答案
名师点拨卷系列答案科目:初中数学 来源:2014-2015学年江苏省泰兴市九年级上学期期中考试数学试卷(解析版) 题型:解答题
(8分)如图所示在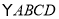 中,
中,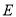 是
是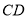 的延长线上一点,
的延长线上一点,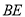 与
与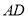 交于点
交于点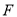 ,
,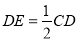 .
.
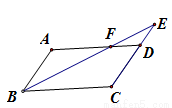
(1)求证: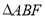 ∽
∽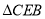 ;
;
(2)若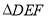 面积为2,求
面积为2,求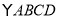 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年河北省沙河市九年级上学期期末模拟考试数学试卷(解析版) 题型:选择题
已知抛物线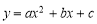 的开口向下,顶点坐标为(2,-3),那么该抛物线有( )
的开口向下,顶点坐标为(2,-3),那么该抛物线有( )
A.最大值 -3 B.最小值-3 C.最小值2 D.最大值2
查看答案和解析>>
科目:初中数学 来源:2014-2015学年河北省沙河市九年级上学期第二次月度联考数学试卷(解析版) 题型:选择题
已知两圆的半径分别是5和8,若两圆相交,则两圆的圆心距可以是( )
A.3 B.8 C.13 D.18
查看答案和解析>>
科目:初中数学 来源:2014-2015学年河北省沙河市九年级上学期第二次月度联考数学试卷(解析版) 题型:选择题
若抛物线y=x2-2x+c与y轴的交点为(0,-3)则该抛物线与x轴的交点是( )
A.(-1,0)和(0,3) B.(0,-1)和(3,0)
C.(-1,0)和(3,0) D.(0,-1)和(0,3)
查看答案和解析>>
科目:初中数学 来源:2014-2015学年河北省沙河市九年级上学期第四次月考数学试卷(解析版) 题型:选择题
如图,在直角坐标系中,正方形OABC的顶点O与原点重合,顶点A.C分别在x轴、y轴上,反比例函数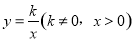 的图象与正方形的两边AB、BC分别交于点M、N,ND⊥x轴,垂足为D,连接OM、ON、MN.下列结论:
的图象与正方形的两边AB、BC分别交于点M、N,ND⊥x轴,垂足为D,连接OM、ON、MN.下列结论:
①△OCN≌△OAM;
②ON=MN;
③四边形DAMN与△MON面积相等;
④若∠MON=450,MN=2,则点C的坐标为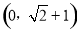 .
.
其中正确的个数是( )
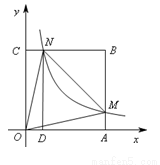
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中数学 来源:2014-2015学年福建省龙岩市九年级上学期半期考试数学试卷(解析版) 题型:解答题
(12分)已知x1,x2是一元二次方程2x2-2x+m+1=0的两个实数根.
(1)求实数m的取值范围;
(2)如果x1,x2满足不等式7+4x1x2>x12+x22,且m为整数,求m的值.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年湖北省咸宁市九年级上学期第二次月考数学试卷(解析版) 题型:选择题
某班同学毕业时都将自己的照片向全班其他同学各送一张表示留念,全班共送1980张照片,如果全班有x名同学,根据题意,列出方程为( ).
A.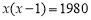 B.
B.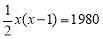
C.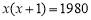 D.
D.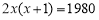
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com