
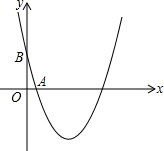
 如图,已知二次函数的图象关于x=-1对称,且最小值为-4,经过A(1,0)、B(0,-3)
如图,已知二次函数的图象关于x=-1对称,且最小值为-4,经过A(1,0)、B(0,-3)分析 (1)由二次函数的图象关于x=-1对称,得到抛物线的对称轴为直线x=-1,求出抛物线与x轴的另一个交点C的坐标为(-3,0),设抛物线解析式为y=a(x+3)(x-1),把B(0,-3)代入解方程即可得到结论;
(2)由于点P在抛物线上,于是设P(x,x2+2x-3),根据已知条件得到方程即可解得结果.
解答 解:(1)∵二次函数的图象关于x=-1对称,
∴抛物线的对称轴为直线x=-1,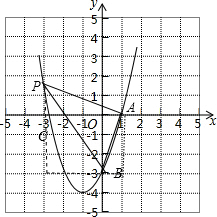
∵二次函数的图象经过A(1,0),
∴抛物线与x轴的另一个交点C的坐标为(-3,0),
设抛物线解析式为y=a(x+3)(x-1),
把B(0,-3)代入得a•3•(-1)=-3,解得a=1,
∴抛物线解析式为y=(x+3)(x-1),即y=x2+2x-3;
(2)存在,设P(x,x2+2x-3),如图,
由题意得:$\frac{1}{2}$(3+x2+2x-3+3)•(1-x)-$\frac{1}{2}$•(-x)•(x2+2x-3+3)-$\frac{1}{2}$•1•3=10,
解得:x1=-4,x2=5,
∴P(-4,5),(5,32).
点评 本题考查了待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.也考查了二次函数图象上点的坐标特征.


科目:初中数学 来源: 题型:选择题
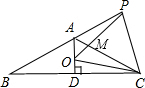 如图,已知等腰△ABC中,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,下面的结论:①∠APO+∠DCO=30°;②△OPC是等边三角形;③AC=AO+AP;④S△ABC=S四边形AOCP,其中正确的个数是( )
如图,已知等腰△ABC中,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,下面的结论:①∠APO+∠DCO=30°;②△OPC是等边三角形;③AC=AO+AP;④S△ABC=S四边形AOCP,其中正确的个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
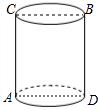 一个无盖圆柱形纸筒的底面周长是60厘米,高是40厘米,如图,一只小蚂蚁在圆筒底部的A处,它想吃到上底面上与点A相对的B点处的蜜糖,
一个无盖圆柱形纸筒的底面周长是60厘米,高是40厘米,如图,一只小蚂蚁在圆筒底部的A处,它想吃到上底面上与点A相对的B点处的蜜糖,查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 四边形ABCD中,AC=BD | |
| B. | 四边形ABCD中,AC⊥BD | |
| C. | 四边形ABCD中,∠A=90°,∠C=90°,∠D=90° | |
| D. | 四边形ABCD中,∠ABC=90° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com