
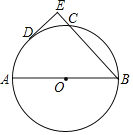
【题目】如图,AB是⊙O的直径,点C、D在半圆上,![]() ,过D作DE⊥BC于E.
,过D作DE⊥BC于E.
(1)求证:DE是⊙O的切线.
(2)若DE=2CE=4,求⊙O的半径.
【答案】(1)证明见解析;(2)5
【解析】
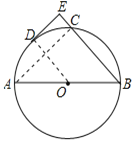
(1)如图,连接OD、AC,由AB是直径可得∠ACB=90°,根据DE⊥BC可得DE//AC,根据垂径定理的推论可得OD⊥AC,即可证明OD⊥DE,由点D在圆上即可证明DE是⊙O的切线;(2)作OF⊥BC于F,可得四边形OFED是矩形,可得OF=DE=4,OD=EF,由垂径定理可得BF=CF,设⊙O的半径为R,在Rt△AOF中,利用勾股定理求出R值即可.
(1)如图,连接OD、AC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴AC⊥BC,
∵DE⊥BC,
∴DE∥AC,
∵![]() ,
,
∴OD⊥AC,
∴DE⊥OD,
∵D在⊙O上,
∴DE是⊙O的切线;
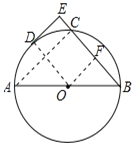
(2)如图,作OF⊥BC于F,
∴BF=CF,
∵DE⊥BE,OD⊥DE,OF⊥BC,
∴四边形OFED是矩形,
∴OF=DE=4,OD=EF,
∵DE=2CE=4,
∴CE=2,
设⊙O的半径为R,则BF=CF=R﹣2,
在Rt△BOF中,BF2+OF2=OA2,
∴(R﹣2)2+42=R2,
解得R=5,
即⊙O的半径为5.


科目:初中数学 来源: 题型:
【题目】某超市一月份的营业额为200万元,一月、二月、三月的营业额共1000万元,如果平均每月增长率为![]() ,则由题意列方程应为____________________________ 。
,则由题意列方程应为____________________________ 。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,⊙M与y轴相切于原点O,平行于x轴的直线交⊙M于P、Q两点,点P在点Q的右边,若P点的坐标为(-1,2),则Q点的坐标是

A. (-4,2) B. (-4.5,2) C. (-5,2) D. (-5.5,2 )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)与y轴交于点C,与x轴交于A、B两点,其中点A的坐标为(4,0),抛物线的对称轴交x轴于点D,CE∥AB,并与抛物线的对称轴交于点E。现有下列结论:①b2-4ac<0;②b>0;③5a+b>0;④BD+CE=4.其中结论正确的个数为( )
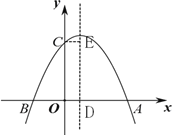
A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:
①4ac<b2;②方程ax2+bx+c=0的两个根是x1=﹣1,x2=3;
③3a+c=0;④当y>0时,x的取值范围是﹣1≤x<3;⑤当x<0时,y随x增大而增大,其中结论正确的是_____(只需填序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】炎热的夏天来临之际.为了调查我校学生消防安全知识水平,学校组织了一次全校的消防安全知识培训,培训完后进行测试,在全校2400名学生中,分别抽取了男生,女生各15份成绩,整理分析过程如下,请补充完整.
(收集数据)
男生15名学生测试成绩统计如下:
68,72,89,85,82,85,74,92,80,85,76,85,69,78,80
女生15名学生测试成绩统计如下:(满分100分)
82,88,83,76,73,78,67,81,82,80,80,86,82,80,82
按如下分数段整理、描述这两组样本数据:
组别 频数 | 65.5~70.5 | 70.5~75.5 | 75.5~80.5 | 80.5~85.5 | 85.5~90.5 | 90.5~95.5 |
男生 | 2 | 2 | 4 | 5 | 1 | 1 |
女生 | 1 | 1 | 5 | 6 | 2 | 0 |
(分析数据)
(1)两组样本数据的平均数、众数、中位数、方差如下表所示:
班级 | 平均数 | 众数 | 中位数 | 方差 |
男生 | 80 | x | 80 | 45.9 |
女生 | 80 | 82 | y | 24.3 |
在表中:x=_____;y=_____.
(2)若规定得分在80分以上(不含80分)为合格,请估计全校学生中消防安全知识合格的学生有______人.
(3)通过数据分析得到的结论是女生掌握消防安全相关知识的整体水平比男生好,请从两个方面说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣x2+bx+c的图象经过点A(﹣1,0),C(0,3).
(1)求二次函数的解析式;
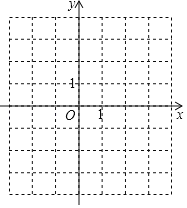
(2)在图中,画出二次函数的图象;
(3)根据图象,直接写出当y≤0时,x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com