
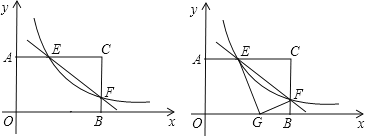
【题目】矩形AOBC中,OB=4,OA=3.分别以OB,OA所在直线为x轴,y轴,建立如图1所示的平面直角坐标系.F是BC边上一个动点(不与B,C重合),过点F的反比例函数y=![]() (k>0)的图象与边AC交于点E.
(k>0)的图象与边AC交于点E.
(1)当点F运动到边BC的中点时,求点E的坐标;
(2)连接EF,求∠EFC的正切值;
(3)如图2,将△CEF沿EF折叠,点C恰好落在边OB上的点G处,求此时反比例函数的解析式.
【答案】(1)E(2,3);(2)![]() ;(3)
;(3)![]() .
.
【解析】(1)先确定出点C坐标,进而得出点F坐标,即可得出结论;
(2)先确定出点F的横坐标,进而表示出点F的坐标,得出CF,同理表示出CF,即可得出结论;
(3)先判断出△EHG∽△GBF,即可求出BG,最后用勾股定理求出k,即可得出结论.
(1)∵OA=3,OB=4,
∴B(4,0),C(4,3),
∵F是BC的中点,
∴F(4,![]() ),
),
∵F在反比例y=![]() 函数图象上,
函数图象上,
∴k=4×![]() =6,
=6,
∴反比例函数的解析式为y=![]() ,
,
∵E点的坐标为3,
∴E(2,3);
(2)∵F点的横坐标为4,
∴F(4,![]() ),
),
∴CF=BC﹣BF=3﹣![]() =
=![]()
∵E的纵坐标为3,
∴E(![]() ,3),
,3),
∴CE=AC﹣AE=4﹣![]() =
=![]() ,
,
在Rt△CEF中,tan∠EFC=![]() ,
,
(3)如图,由(2)知,CF=![]() ,CE=
,CE=![]() ,
,![]() ,
,
过点E作EH⊥OB于H,
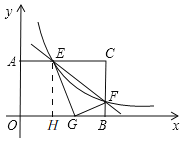
∴EH=OA=3,∠EHG=∠GBF=90°,
∴∠EGH+∠HEG=90°,
由折叠知,EG=CE,FG=CF,∠EGF=∠C=90°,
∴∠EGH+∠BGF=90°,
∴∠HEG=∠BGF,
∵∠EHG=∠GBF=90°,
∴△EHG∽△GBF,
∴![]() ,
,
∴![]() ,
,
∴BG=![]() ,
,
在Rt△FBG中,FG2﹣BF2=BG2,
∴(![]() )2﹣(
)2﹣(![]() )2=
)2=![]() ,
,
∴k=![]() ,
,
∴反比例函数解析式为y=![]() .
.


科目:初中数学 来源: 题型:
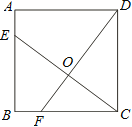
【题目】如图,已知正方形ABCD的边长为4,点E、F分别在边AB、BC上,且AE=BF=1,CE、DF交于点O.下列结论:①∠DOC=90°, ②OC=OE, ③tan∠OCD =![]() ,④
,④![]() 中,正确的有( )
中,正确的有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校七年级一班和二班各派出10名学生参加一分钟跳绳比赛,成绩如下表:
跳绳成绩(个) | 132 | 133 | 134 | 135 | 136 | 137 |
一班人数(人) | 1 | 0 | 1 | 5 | 2 | 1 |
二班人数(人) | 0 | 1 | 4 | 1 | 2 | 2 |
(1)两个班级跳绳比赛成绩的众数、中位数、平均数、方差如下表:
众数 | 中位数 | 平均数 | 方差 | |
一班 | a | 135 | 135 | c |
二班 | 134 | b | 135 | 1.8 |
表中数据a= ,b= ,c= ;
(2)请用所学的统计知识,从两个角度比较两个班跳绳比赛的成绩.
查看答案和解析>>
科目:初中数学 来源: 题型:
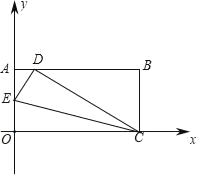
【题目】将一矩形纸片OABC放在直角坐标系中,O为原点C在x轴上,OA=5,OC=13,如图所示,在OA上取一点E,将△EOC沿EC折叠,使O点落在AB边上的D点,则E点坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 和
和![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
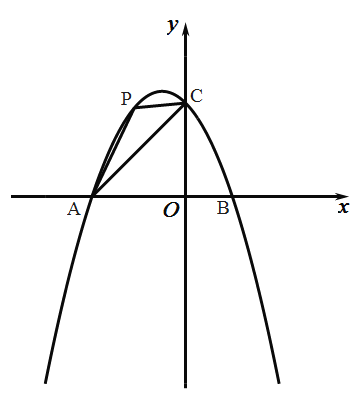
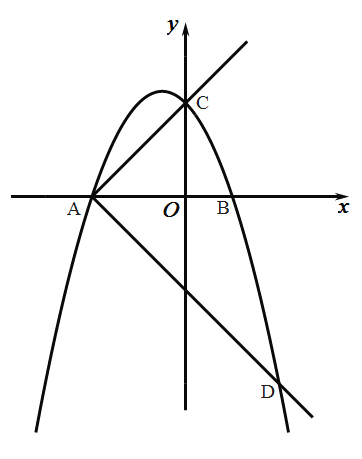
(1)求抛物线的表达式;
(2)点![]() 是抛物线上第二象限内的点,连接
是抛物线上第二象限内的点,连接![]() ,设
,设![]() 的面积为
的面积为![]() ,当
,当![]() 取最大值时,求点
取最大值时,求点![]() 的坐标;
的坐标;
(3)作射线![]() ,将射线
,将射线![]() 绕
绕![]() 点顺时针旋转
点顺时针旋转![]() 交抛物线于另一点
交抛物线于另一点![]() ,在射线
,在射线![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() 的周长最小.若存在,求出
的周长最小.若存在,求出![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
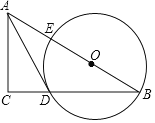
【题目】如图,在Rt△ABC中,点O在斜边AB上,以O为圆心,OB为半径作圆,分别与BC,AB相交于点D,E,连结AD.已知∠CAD=∠B,
(1)求证:AD是⊙O的切线.
(2)若BC=8,tanB=![]() ,求⊙O 的半径.
,求⊙O 的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图为住宅区内的两幢楼,它们的高AB=CD=30m,两楼之间的距离AC=24m,现需了解甲楼对乙楼的采光的影响情况,当太阳光与水平线的夹角为30°时,求甲楼的影子在乙楼上有多高?(精确到0.1m,![]() ≈1.41,
≈1.41,![]() ≈1.73)?
≈1.73)?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将矩形纸片![]() 沿对角线
沿对角线![]() 翻折,使点
翻折,使点![]() 的对应点
的对应点![]() (落在矩形
(落在矩形![]() 所在平面内,
所在平面内,![]() 与
与![]() 相交于点
相交于点![]() ,接
,接![]() .
.
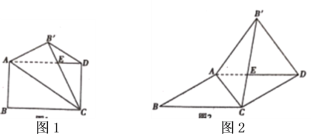
(1)在图1中,
①![]() 和
和![]() 的位置关系为__________________;
的位置关系为__________________;
②将![]() 剪下后展开,得到的图形是_________________;
剪下后展开,得到的图形是_________________;
(2)若图1中的矩形变为平行四边形时(![]() ),如图2所示,结论①、②是否成立,若成立,请对结论②加以证明,若不成立,请说明理由
),如图2所示,结论①、②是否成立,若成立,请对结论②加以证明,若不成立,请说明理由
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com