
【题目】已知二次函数y=9x2﹣6ax+a2﹣b
(1)当b=﹣3时,二次函数的图象经过点(﹣1,4)
①求a的值;
②求当a≤x≤b时,一次函数y=ax+b的最大值及最小值;
(2)若a≥3,b﹣1=2a,函数y=9x2﹣6ax+a2﹣b在﹣![]() <x<c时的值恒大于或等于0,求实数c的取值范围.
<x<c时的值恒大于或等于0,求实数c的取值范围.
【答案】(1)①a的值是﹣2或﹣4;②当x=﹣4时,函数取得最大值,y=13,当x=﹣3时,函数取得最小值,y=9;(2)﹣![]() <c≤
<c≤![]() .
.
【解析】
(1)①把b=﹣3和点(﹣1,4)代入y=9x2﹣6ax+a2﹣b即可求出a的值;②根据a≤x≤b,b=﹣3求出a的值,然后根据一次函数的性质求解即可;
(2)先求出抛物线与x轴的交点,然后根据﹣![]() <x<c时的值恒大于或等于0列式求解即可.
<x<c时的值恒大于或等于0列式求解即可.
(1)①∵y=9x2﹣6ax+a2﹣b,当b=﹣3时,
二次函数的图象经过点(﹣1,4)
∴4=9×(﹣1)2﹣6a×(﹣1)+a2+3,
解得,a1=﹣2,a2=﹣4,
∴a的值是﹣2或﹣4;
②∵a≤x≤b,b=﹣3
∴a=﹣2舍去,
∴a=﹣4,
∴﹣4≤x≤﹣3,
∴一次函数y=﹣4x﹣3,
∵一次函数y=﹣4x﹣3中,y随x的增大而减小,
∴当x=﹣4时,函数取得最大值,y=﹣4×(﹣4)﹣3=13
x=﹣3时,函数取得最小值,y=﹣4×(﹣3)﹣3=9
(2)∵b﹣1=2a
∴y=9x2﹣6ax+a2﹣b可化简为y=9x2﹣6ax+a2﹣2a﹣1
∴抛物线的对称轴为:x=![]() ≥1,
≥1,
抛物线与x轴的交点为(![]() ,0)(
,0)(![]() ,0)
,0)
∵函数y=9x2﹣6ax+a2﹣b在﹣![]() <x<c时的值恒大于或等于0
<x<c时的值恒大于或等于0
∴c≤![]() ,
,
∵a≥3,
∴﹣![]() <c≤
<c≤![]() .
.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图所示是一个直角三角形的苗圃,由一个正方形花坛和两块直角三角形的草皮组成.如果两个直角三角形的两条斜边长分别为4米和6米,则草皮的总面积为( )平方米.
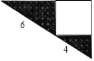
A. 3![]() B. 9 C. 12 D. 24
B. 9 C. 12 D. 24
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2-2ax+c(a≠0)与y轴交于点C(0,4),与x轴交于点A、B,点A的坐标为(4,0).
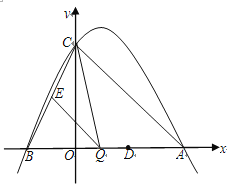
(1)求该抛物线的解析式;
(2)点Q是线段AB上的动点,过点Q作QE∥AC,交BC于点E,连接CQ,当△CQE的面积为3时,求点Q的坐标;
(3)若平行于x轴的动直线l与该抛物线交于点P,与直线AC交于点F,点D的坐标为(2,0).问:是否存在这样的直线l,使得△ODF是等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,分别是两棵树及其影子的情形
(1)哪个图反映了阳光下的情形?哪个图反映了路灯下的情形.
(2)请画出图中表示小丽影长的线段.
(3)阳光下小丽影子长为1.20m树的影子长为2.40m,小丽身高1.88m,求树高.

查看答案和解析>>
科目:初中数学 来源: 题型:
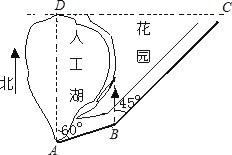
【题目】初三(5)班综合实践小组去湖滨花园测量人工湖的长,如图A、D是人工湖边的两座雕塑,AB、BC是湖滨花园的小路,小东同学进行如下测量,B点在A点北偏东60°方向,C点在B点北偏东45°方向,C点在D点正东方向,且测得AB=20米,BC=40米,求AD的长.(![]() ≈1.732,
≈1.732,![]() ≈1.414,结果精确到0.01米)
≈1.414,结果精确到0.01米)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,甲物体高4米,影长3米,乙物体高2米,影长4米,两物体相距5米.
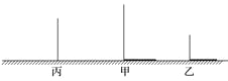
(1)在图中画出灯的位置,并画出丙物体的影子.
(2)若灯杆,甲、乙都与地面垂直并且在同一直线上,试求出灯的高度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com