
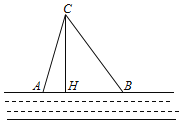
����Ŀ����һ����������ӵ�һ����һ��ׯC���ӱ�ԭ������ȡˮ��A��B������AB��AC������ij��ԭ����C��A��·�����Ѿ���ͨ���ô�Ϊ�������ȡˮ�����ںӱ��½�һ��ȡˮ��H��A��H��B��ͬһ��ֱ���ϣ���������һ��·CH�����CB��2.5ǧ�ף�CH��2ǧ�ף�HB��1.5ǧ�ף�
��1����CH�Ƿ�Ϊ�Ӵ�ׯC���ӱߵ����·����ͨ���������˵����
��2����ԭ����·��AC�ij�������ȷ��0.01��
���𰸡���1���ǣ�����������2��2.08ǧ��
��������
��1��������ֱ�Ӹ��ݹ��ɶ������涨����ɣ�
��2��������ֱ�Ӹ��ݹ��ɶ�����ɣ�
�⣺��1���ǣ��������£�
����CHB��CB��2.5��CH��2��HB��1.5��
��CH2+HB2��22+1.52��6.25��CB2��2.52��6.25��
��CH2+HB2��CB2��
��CH��AB��
��CH�ǴӴ�ׯC���ӱߵ����·��
��2����AC��xǧ�ף���AB��AC��xǧ�ף�AH��x��1.5��ǧ�ף�
��Rt��AHC�У��ɹ��ɶ����ã�AH2+HC2��AC2
��x2����x��1.5��2+22
��ã�x��2.08
��ԭ����·��AC�ij�ԼΪ2.08ǧ�ף�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������С������11������ͼ����֪������![]() �Ķ���D������Ϊ��1��
�Ķ���D������Ϊ��1��![]() ��������x�ύ��A��B���㣬��y�ύ��C�㣬A�������Ϊ��4��0����P�����������ϵ�һ�����㣬�Һ�����Ϊm��
��������x�ύ��A��B���㣬��y�ύ��C�㣬A�������Ϊ��4��0����P�����������ϵ�һ�����㣬�Һ�����Ϊm��
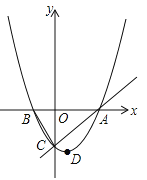
��l��������������Ӧ�Ķ��κ����ı���ʽ��
��2��������P������PAO������45������P��ĺ�����m��ȡֵ��Χ��
��3����P��ĺ�����![]() ʱ����p����y��Ĵ���PQ������ΪQ���ʣ��Ƿ����P�㣬ʹ��QPO=��BCO�������ڣ������P������ꣻ�������ڣ���˵�����ɣ�
ʱ����p����y��Ĵ���PQ������ΪQ���ʣ��Ƿ����P�㣬ʹ��QPO=��BCO�������ڣ������P������ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
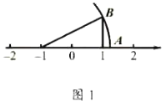
����Ŀ����1����ͼ1��![]() �У�
��![]() ����
����![]() ������-1������
������-1������![]() ������1����
������1����![]() ��
��![]() ���������ϵ�
���������ϵ�![]() ��Ӧ������ ��
��Ӧ������ ��
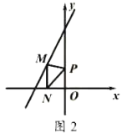
��2����ͼ2����![]() ��ֱ��
��ֱ��![]() �ϵĶ��㣬����
�ϵĶ��㣬����![]() ��
��![]() ��ֱ
��ֱ![]() ���ڵ�
���ڵ�![]() ����
����![]() ��
��![]() ���ϵĶ��㣬����
���ϵĶ��㣬����![]() ��
��![]() ��
��![]() Ϊ�����������Ϊ����ֱ��������ʱ��
Ϊ�����������Ϊ����ֱ��������ʱ��![]() ������Ϊ ��
������Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ʦ��������ҵ��������һ����ʽ�ļ����⣺![]() ���ס�����λͬѧ��ɵĹ��̷ֱ����£�
���ס�����λͬѧ��ɵĹ��̷ֱ����£�
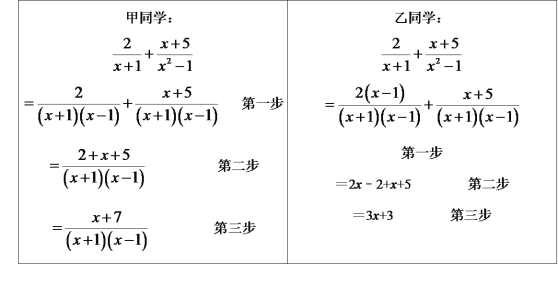
��ʦ��������λͬѧ�Ľ���д���
����Ӽס�����λͬѧ�У�ѡ��һλͬѧ�Ľ����̣������������������Ը�����
��1����ѡ���������� ͬѧ�Ľ����̽��з���������ס����ҡ�����ͬѧ�Ľ��ӵ��������� ����ʼ���ִ������ԭ������������ ��
��2��������д����ɴ������ȷ�����̣�
![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1����֪���κ���![]() ��ͼ���㣨��2��8���ͣ���1��5������������κ����ı���ʽ��
��ͼ���㣨��2��8���ͣ���1��5������������κ����ı���ʽ��
��2����֪�����ߵĶ���Ϊ����1����3������y��Ľ���Ϊ��0����5�����������������Ӧ�ĺ�������ʽ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͼ��ʾ�������������У�ÿ��С�����εı߳�Ϊ![]() ����������Σ������������ߵĽ���������Σ�
����������Σ������������ߵĽ���������Σ�![]() �Ķ���
�Ķ���![]() ��
��![]() ������ֱ�Ϊ
������ֱ�Ϊ![]() ��
��![]() ��
��
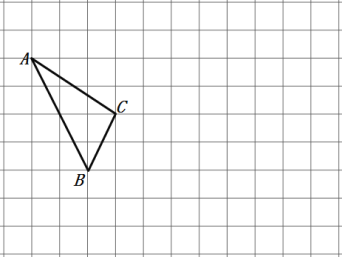
��1��������ͼ��ʾ������������![]() �ᡢ
�ᡢ![]() �
�
��2��������![]() ����
����![]() ��ԳƵ�
��ԳƵ�![]() ����д����������д����
����д����������д����![]() �����ꣻ
�����ꣻ
��3�����![]() ����
����![]() ��ԳƵ�
��ԳƵ�![]() �������
�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ƽ��ֱ������ϵ�У���A��B��C��x���ϣ���D��E��y���ϣ�OA=OD=2��OC=OE=4��BΪ�߶�OA���е㣬ֱ��AD�뾭��B��E��C����������߽���F��G���㣬����Գ��ύ��M����PΪ�߶�FG��һ�����㣨��F��G���غϣ���PQ��y���������߽��ڵ�Q��
��1����B��E��C����������ߵĽ���ʽ��
��2���жϡ�BDC����״��������֤������P��ʲôλ��ʱ����P��O��CΪ������������ǵ��������Σ��������ʱ��P�����ꣻ
��3���������ߵĶ���ΪN������QN��̽���ı���PMNQ����״�����ܷ��Ϊ���Σ����ܷ��Ϊ�������Σ����ܣ���ֱ��д����P�����ꣻ�����ܣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ����߷���������ij���ݾ����Լס��������������Ǽ���������֪�������������ñ�����������������3��Ԫ�����������ͬ��������������������Ϊ625��Ԫ������������Ϊ700��Ԫ��
��1���ס���������ÿ���������ø�������Ԫ��
��2�������Ҫ�ס�����������80�ף����������ʽ�����2090��Ԫ����������2096��Ԫ���������ʽ�ȫ�����ڼס��������Ǽ����������������������������м��ַ�������һ�ַ����������������٣�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com