
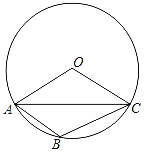
【题目】如图,△ABC内接于⊙O,∠AOC=∠ABC,AC=5,则⊙O的半径长为_____.
【答案】![]() .
.
【解析】
作![]() 所对的圆周角∠APC,作OH⊥AC于H,根据圆周角定理和圆内接四边形的性质可得∠AOC=120°,则∠OAC=∠OCA=30°,再根据垂径定理得到AH=CH=
所对的圆周角∠APC,作OH⊥AC于H,根据圆周角定理和圆内接四边形的性质可得∠AOC=120°,则∠OAC=∠OCA=30°,再根据垂径定理得到AH=CH=![]() AC=
AC=![]() ,最后根据直角三角形30度所对的边为斜边的一半即可解答.
,最后根据直角三角形30度所对的边为斜边的一半即可解答.
解:作![]() 所对的圆周角∠APC,作OH⊥AC于H,如图,
所对的圆周角∠APC,作OH⊥AC于H,如图,
∵∠APC+∠ABC=180°,∠AOC=2∠APC,
∴![]() ∠AOC+∠ABC=180°,
∠AOC+∠ABC=180°,
∵∠AOC=∠ABC,
∴![]() ∠AOC+∠AOC=180°,解得∠AOC=120°,
∠AOC+∠AOC=180°,解得∠AOC=120°,
∴∠OAC=∠OCA=30°,
∵OH⊥AC,
∴AH=CH=![]() AC=
AC=![]() ,
,
在Rt△OAH中,OH=![]() AH=
AH=![]() ,
,
∴OA=2OH=![]() ,
,
即⊙O的半径长为![]() .
.
故答案为![]() .
.



科目:初中数学 来源: 题型:
【题目】某商品的进价为每件40元,售价为每件50元,每个月可卖出210件,如果每件商品的售价每上涨1元,则每个月少卖10件(每件售价不能高于65元),设每件商品的售价上涨x元(x为正整数),每个月的销售利润为y元.
(1)求y与x的函数关系式并直接写出自变量x的取值范围;
(2)每件商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?
(3)若在销售过程中每一件商品有a(a>1)元的其他费用,商家发现当售价每件不低于57元时,每月的销售利润随x的增大而减小,请直接写出a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两超市(大型商场)同时开业,为了吸引顾客,都举行有奖酬宾活动:凡购物满![]() 元,均可得到一次摸奖的机会.在一个纸盒里装有
元,均可得到一次摸奖的机会.在一个纸盒里装有![]() 个红球和
个红球和![]() 个白球(编号分别为红1、红
个白球(编号分别为红1、红![]() 、白1、白
、白1、白![]() ),除颜色外其它都相同,摸奖者一次从中摸出两个球,根据球的颜色决定送礼金券(在他们超市使用时,与人民币等值)的多少(如表)
),除颜色外其它都相同,摸奖者一次从中摸出两个球,根据球的颜色决定送礼金券(在他们超市使用时,与人民币等值)的多少(如表)
甲超市:
球 | 两红 | --红一白 | 两白 |
礼金券(元) |
|
|
|
乙超市:
球 | 两红 | --红一白 | 两白 |
礼金券(元) |
|
|
|
(1)列举出一次摸奖时两球的所有情况;
(2)如果只考虑中奖因素,你将会选择去哪个超市购物?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】超市销售某种儿童玩具,如果每件利润为40元(市场管理部门规定,该种玩具每件利润不能超过60元),每天可售出50件.根据市场调查发现,销售单价每增加2元,每天销售量会减少1件.设销售单价增加![]() 元,每天售出
元,每天售出![]() 件.
件.
(1)请写出![]() 与
与![]() 之间的函数表达式;
之间的函数表达式;
(2)当![]() 为多少时,超市每天销售这种玩具可获利润2250元?
为多少时,超市每天销售这种玩具可获利润2250元?
(3)设超市每天销售这种玩具可获利![]() 元,当
元,当![]() 为多少时
为多少时![]() 最大,最大值是多少?
最大,最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小亮晚上在广场散步,图中线段AB表示站立在广场上的小亮,线段PO表示直立在广场上的灯杆,点P表示照明灯的位置.
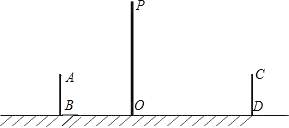
(1)请你在图中画出小亮站在AB处的影子BE;
(2)小亮的身高为1.6m,当小亮离开灯杆的距离OB为2.4m时,影长为1.2m,若小亮离开灯杆的距离OD=6m时,则小亮(CD)的影长为多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地教育部门为学生提供了四种在线学习方式:阅读、听课、答疑、讨论,并对部分学生作了“最感兴趣的在线学习方式”网络调查(只选择一类),把调查结果绘制成如下两幅尚不完整的统计图:

根据图中信息,回答下列问题:
(1)本次调查的人数有 人;在扇形统计图中,“在线答疑”所在扇形的圆心角度数是 ;
(2)补全条形统计图;
(3)在随机调查的学生中,甲、乙两位同学选择同类“最感兴趣的在线学习方式”的概率是否等于![]() ?说明理由.
?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2+bx+c与x轴交于A(﹣1,0)和B(3,0)两点,交y轴于点E.
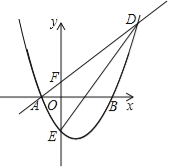
(1)求此抛物线的解析式.
(2)若直线y=x+1与抛物线交于A、D两点,与y轴交于点F,连接DE,求△DEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
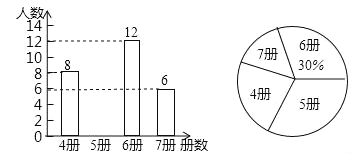
【题目】高尔基说:“书,是人类进步的阶梯.”阅读可以丰富知识、拓展视野、充实生活等诸多益处.为了解学生的课外阅读情况,某校随机抽查了部分学生阅读课外书册数的情况,并绘制出如下统计图,其中条形统计图因为破损丢失了阅读5册书数的数据.
(1)求条形图中丢失的数据,并写出阅读书册数的众数和中位数;
(2)根据随机抽查的这个结果,请估计该校1200名学生中课外阅读5册书的学生人数;
(3)若学校又补查了部分同学的课外阅读情况,得知这部分同学中课外阅读最少的是6册,将补查的情况与之前的数据合并后发现中位数并没有改变,试求最多补查了多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为2的正方形ABCD中,AE平分∠DAC,AE交CD于点F,CE⊥AE,垂足为点E,EG⊥CD,垂足为点G,点H在边BC上,BH=DF,连接AH、FH,FH与AC交于点M.下面结论:①FH=2BH;②AC⊥FH;③DF=1;④ EG2=FGDG.其中正确的个数为( )
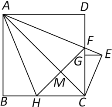
A.1B.2C.3D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com