
����Ŀ�����գ���У���꼶ͬѧ�������������ԣ�Ϊ�˽��ҵ��������������һ������С����������˲���ͬѧ�IJ��Գɼ������������Ϊ���š��������������С�������ĸ��ȼ����ֱ����![]() ��
��![]() ��
��![]() ��
��![]() �����ݵ��������Ƴ���ͼ��ʾ������ͳ��ͼ������ͳ��ͼ��δ���ƣ�������ͼ��������Ϣ����������⣺
�����ݵ��������Ƴ���ͼ��ʾ������ͳ��ͼ������ͳ��ͼ��δ���ƣ�������ͼ��������Ϣ����������⣺
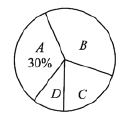
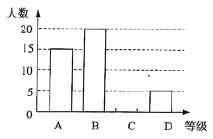
��1�����ε����ѧ������Ϊ �ˣ�
��2��������ͳ��ͼ�У�![]() ����Ӧ���ε�Բ�Ľ� �ȣ���������ͳ��ͼ����������
����Ӧ���ε�Բ�Ľ� �ȣ���������ͳ��ͼ����������
��3���ڡ��š��͡����������ȼ���ͬѧ����������Ը����ܽ�һ��ѵ�����ִ���������ѡ����λ����ѵ���������б�������״ͼ�ķ����������ѡ����λͬѧ���Գɼ�ǡ�ö�Ϊ�������ĸ��ʣ�
���𰸡���1��50����2��144����ͼ����������3��![]() ��
��
��������
��1����������������������ռ�İٷֱȼ��������������
��2����360��������������ռ�İٷֱ����B����Ӧ���ε�Բ�Ľǣ�����������ȥ��������������������������������������������������ɲ�ȫͳ��ͼ��
��3���������⻭����״ͼ�ó����Ե����������ѡ����λͬѧ���Գɼ�ǡ�ö�Ϊ���������������Ȼ����ݸ��ʹ�ʽ���ɵó��𰸣�
��1�����ε����ѧ������Ϊ��15��30%=50���ˣ���
�ʴ�Ϊ��50��
��2��������ͳ��ͼ�У�B����Ӧ���ε�Բ�Ľ���360���![]() =144����
=144����
�������ȼ��������ǣ�50-15-20-5=10���ˣ�����ͼ���£�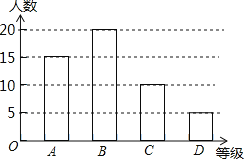
�ʴ�Ϊ��10��
��3�������������������ķֱ���A1��A2����B1��B2��ʾ������״ͼ���£�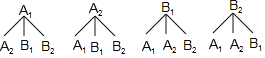
����12���������ѡ����λͬѧ���Գɼ�ǡ�ö�Ϊ����������2�֣�
����ѡ����λͬѧ���Գɼ�ǡ�ö�Ϊ�������ĸ�����![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ABC��ֱ������ƽ���ڣ��������������ֱ�ΪA��1��0����B��3��2����C��0��1����������������ÿ��С�����εı߳���һ����λ���ȣ���
(1)��x������ƽ��2����λ���õ���A1B1C1������ͼֱ��д�������仯���![]() ������ꡣ��
������ꡣ��![]() ������������
������������
(2)��A��Ϊλ������,�������ڻ�����A2B2C2��ʹ��A2B2C2����ABCλ�ƣ���λ�Ʊ�Ϊ2��1�����![]() ��������������
��������������
(3) ��A2B2C2���������ƽ����λ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
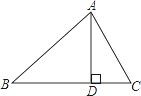
����Ŀ����ͼ����ABC�У�AD��BC��D�������������١�B+��DAC=90�㣻�ڡ�B=��DAC����![]() =
=![]() ����AB2=BDBC������һ���ܹ��ж���ABC��ֱ�������ε��У� ��
����AB2=BDBC������һ���ܹ��ж���ABC��ֱ�������ε��У� ��
A. 1 B. 2 C. 3 D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
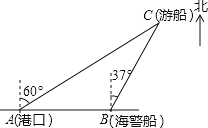
����Ŀ�� һ�ҹ۹��δ��Ӹۿ�A�Ա�ƫ��60��ķ�����۹۹⣬����80������C��ʱ�����˲෭�����¹ʣ���������������źţ�һ���ڸۿ���������ĺ������ӵ�����źţ�����¹ʴ������ı�ƫ��37�㷽��������40����ÿСʱ���ٶ�ǰ����Ԯ�����������¹ʴ�C������Ĵ�Լʱ�䣮����ܰ��ʾ��sin53���0.8��cos53���0.6��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�����������̡��������г�������2020��ijͬѧ�������г�������![]() ��
��![]() ����ԭ���ϣ�
����ԭ���ϣ�![]() �ĵ���Ϊÿ��6Ԫ��
�ĵ���Ϊÿ��6Ԫ��![]() �ĵ���Ϊÿ��3Ԫ����ͬѧ�Ĵ�����Ʒ��Ҫ
�ĵ���Ϊÿ��3Ԫ����ͬѧ�Ĵ�����Ʒ��Ҫ![]() ���ϵ�������
���ϵ�������![]() ����������2����ͬʱ��Ϊ�˼��ٳɱ�����ͬѧ����ԭ���ϵ��ܷ��ò�����480Ԫ��
����������2����ͬʱ��Ϊ�˼��ٳɱ�����ͬѧ����ԭ���ϵ��ܷ��ò�����480Ԫ��
��1����ͬѧ������ټ�![]() ���ϣ�
���ϣ�
��2���ڸ�ͬѧ����![]() ��������ǰ���£����������
��������ǰ���£����������![]() ��
��![]() ���ֲ���ȫ��������Ʒ�����������������ù�����520Ԫ������죬��ͬѧ�ڳɱ��ۣ�������Ϸ���+�������ã��Ļ������������
���ֲ���ȫ��������Ʒ�����������������ù�����520Ԫ������죬��ͬѧ�ڳɱ��ۣ�������Ϸ���+�������ã��Ļ������������![]() ��ۣ��������ʽ����Ǹ�ͬѧ�ڱ�۵Ļ����Ͻ���
��ۣ��������ʽ����Ǹ�ͬѧ�ڱ�۵Ļ����Ͻ���![]() ���ۣ����գ��ڻ����ʱ��Ʒ���꣬��������ͬѧ�ڱ��λ����
���ۣ����գ��ڻ����ʱ��Ʒ���꣬��������ͬѧ�ڱ��λ����![]() ����
����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�н����п�����ʵ��������ԣ�����ѧ����ǩ��ʽ�����Լ��Ŀ������ݣ��涨ÿλ������������������ʵ�飨��ֽǩA��B��C��ʾ����������ѧ���飨��ֽǩD��E��F��ʾ���и���ȡһ��ʵ��������п��ԣ�С���ڿ�����ֽǩ������£��ֱ���и������ȡһ�������б�����״ͼ�ķ�����С�ճ鵽����ʵ��B�ͻ�ѧʵ��F�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
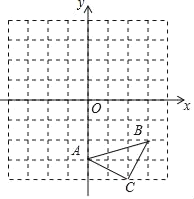
����Ŀ����ͼ����ABC�������������ֱ�ΪA��0����3����B��3����2����C��2����4�����������������У�ÿ��С�����εı߳���1����λ���ȣ�
��1��������ABC����ƽ��4����λ�õ��ġ�A1B1C1��
��2���Ե�CΪλ�����ģ��������л�����A2B2C��ʹ��A2B2C���ABCλ�ƣ��ҡ�A2B2C���ABC��λ�Ʊ�Ϊ2��1����ֱ��д����B2�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��ֱ��AB��y����3x+3���������ύ��A��B���㣮
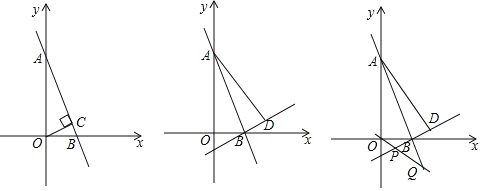
��1������O��OC��AB�ڵ�C����OC�ij���
��2������AOB��AB���۵���ABD����O���D��Ӧ����ֱ��BD�Ľ���ʽ��
��3���ڣ�2���������£�����������y��kx��ֱ��BD����P��ֱ��AB����Q����OP��3OQ���������������Ľ���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
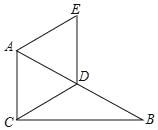
����Ŀ����ͼ����֪Rt��ABC�У���ACB��90�㣬��B��30�㣬D��AB���е㣬AE��CD��AC��ED��
��֤���ı���ACDE�����Σ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com