
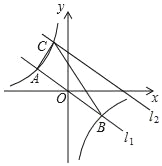
【题目】如图,在平面直角坐标系中,直线l1:y=﹣![]() x与反比例函数y=
x与反比例函数y=![]() 的图象交于A,B两点(点A在点B左侧),已知A点的纵坐标是2;
的图象交于A,B两点(点A在点B左侧),已知A点的纵坐标是2;
(1)求反比例函数的表达式;
(2)根据图象直接写出﹣![]() x>
x>![]() 的解集;
的解集;
(3)将直线l1:y=- ![]() x沿y向上平移后的直线l2与反比例函数y=
x沿y向上平移后的直线l2与反比例函数y=![]() 在第二象限内交于点C,如果△ABC的面积为30,求平移后的直线l2的函数表达式.
在第二象限内交于点C,如果△ABC的面积为30,求平移后的直线l2的函数表达式.
【答案】(1) y=﹣![]() ;(2) x<﹣4 或 0<x<4;(3) y=-
;(2) x<﹣4 或 0<x<4;(3) y=-![]() .
.
【解析】
(1)直线l1:y= -![]() x经过点A,且A点的纵坐标是2,可得A(-4,2),代入反比例函数解析式可得k的值;(2)根据图象得到点B的坐标,进而直接得到﹣
x经过点A,且A点的纵坐标是2,可得A(-4,2),代入反比例函数解析式可得k的值;(2)根据图象得到点B的坐标,进而直接得到﹣ ![]() x>
x> ![]() 的解集即可;(3)设平移后的直线
的解集即可;(3)设平移后的直线 ![]() 与 x 轴交于点 D,连接 AD,BD,由平行线的性质可得出S△ABC=S△ABF,即可得出关于OD的一元一次方程,解方程即可得出结论.
与 x 轴交于点 D,连接 AD,BD,由平行线的性质可得出S△ABC=S△ABF,即可得出关于OD的一元一次方程,解方程即可得出结论.
(1)∵直线 l1:y=﹣![]() x 经过点 A,A 点的纵坐标是 2,
x 经过点 A,A 点的纵坐标是 2,
∴当 y=2 时,x=﹣4,
∴A(﹣4,2),
∵反比例函数 y=![]() 的图象经过点 A,
的图象经过点 A,
∴k=﹣4×2=﹣8,
∴反比例函数的表达式为 y=﹣![]() ;
;
(2)∵直线 l1:y=﹣![]() x 与反比例函数 y=
x 与反比例函数 y=![]() 的图象交于 A,B 两点,
的图象交于 A,B 两点,
∴B(4,﹣2),
∴不等式﹣ ![]() x>
x> ![]() 的解集为 x<﹣4 或 0<x<4;
的解集为 x<﹣4 或 0<x<4;
(3)如图,设平移后的直线 ![]() 与 x 轴交于点 D,连接 AD,BD,
与 x 轴交于点 D,连接 AD,BD,
∵CD∥AB,
∴△ABC 的面积与△ABD 的面积相等,
∵△ABC 的面积为 30,
∴S△AOD+S△BOD=30,即 ![]() OD(|yA|+|yB|)=30,
OD(|yA|+|yB|)=30,
∴![]() ×OD×4=30,
×OD×4=30,
∴OD=15,
∴D(15,0),
设平移后的直线 ![]() 的函数表达式为 y=﹣
的函数表达式为 y=﹣![]() x+b, 把 D(15,0)代入,可得 0=﹣
x+b, 把 D(15,0)代入,可得 0=﹣![]() ×15+b,
×15+b,
解得 b=![]() ,
,
∴平移后的直线![]() 的函数表达式为 y=-
的函数表达式为 y=-![]() .
.


 寒假学与练系列答案
寒假学与练系列答案科目:初中数学 来源: 题型:
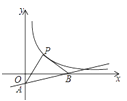
【题目】如图,直线y=![]() x﹣1与坐标轴交于A,B两点,点P是曲线y=
x﹣1与坐标轴交于A,B两点,点P是曲线y=![]() (x>0)上一点,若△PAB是以∠APB=90°的等腰三角形,则k= _________.
(x>0)上一点,若△PAB是以∠APB=90°的等腰三角形,则k= _________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着人们生活水平的不断提高,旅游已成为人们的一种生活时尚.为 开发新的旅游项目,我市对某山区进行调查,发现一瀑布.为测量它的高度,测 量人员在瀑布的对面山上 D 点处测得瀑布顶端 A 点的仰角是 30°,测得瀑布底端 B 点的俯角是 10°,AB 与水平面垂直.又在瀑布下的水平面测得 CG=27m, GF=17.6m(注:C、G、F 三点在同一直线上,CF⊥AB 于点 F).斜坡 CD=20m, 坡角∠ECD=40°.求瀑布 AB 的高度.(参考数据:![]() ≈1.73,sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,sin10°≈0.17,cos10°≈0.98,tan10°≈0.18)
≈1.73,sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,sin10°≈0.17,cos10°≈0.98,tan10°≈0.18)

查看答案和解析>>
科目:初中数学 来源: 题型:
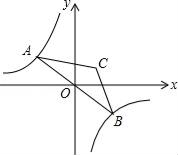
【题目】如图,点A是双曲线y=﹣![]() 在第二象限分支上的一个动点,连接AO并延长交另一分支于点B,以AB为底作等腰△ABC,且∠ACB=120°,点C在第一象限,随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=
在第二象限分支上的一个动点,连接AO并延长交另一分支于点B,以AB为底作等腰△ABC,且∠ACB=120°,点C在第一象限,随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=![]() 上运动,则k的值为_____.
上运动,则k的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
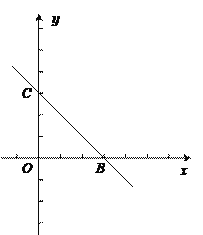
【题目】如图,在平面直角坐标系xOy中,直线BC与抛物线y=x2+bx+c交于点B(3,0)和点C(0,3),抛物线y=x2+bx+c过点B、C且与x轴的另一个交点为A.
(1)求直线BC及该抛物线的表达式;
(2)设该抛物线的顶点为D,求△DBC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
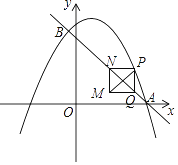
【题目】如图,在平面直角坐标系中,直线y=﹣x+3与抛物线![]() 交于A、B两点,点A在x轴上,点B的横坐标为
交于A、B两点,点A在x轴上,点B的横坐标为![]() .动点P在抛物线上运动(不与点A、B重合),过点P作y轴的平行线,交直线AB于点Q.当PQ不与y轴重合时,以PQ为边作正方形PQMN,使MN与y轴在PQ的同侧,连结PM.设点P的横坐标为m.
.动点P在抛物线上运动(不与点A、B重合),过点P作y轴的平行线,交直线AB于点Q.当PQ不与y轴重合时,以PQ为边作正方形PQMN,使MN与y轴在PQ的同侧,连结PM.设点P的横坐标为m.
(1)求b、c的值.
(2)当点N落在直线AB上时,直接写出m的取值范围.
(3)当点P在A、B两点之间的抛物线上运动时,设正方形PQMN的周长为C,求C与m之间的函数关系式,并写出C随m增大而增大时m的取值范围.
(4)当△PQM与坐标轴有2个公共点时,直接写出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点 P(x,y)在第一象限,且 x+y=12,点 A(10,0)在 x 轴上,当△OPA 为直角三角形时,点 P 的坐标为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】假设北碚万达广场地下停车场有5个出入口,每天早晨6点开始对外停车且此时车位空置率为75%,在每个出入口的车辆数均是匀速出入的情况下,如果开放2个进口和3个出口,8小时车库恰好停满;如果开放3个进口和2个出口,2小时车库恰好停满.2019年元旦节期间,由于商场人数增多,早晨6点时的车位空置率变为60%,又因为车库改造,只能开放2个进口和1个出口,则从早晨6点开始经过________小时车库恰好停满.
查看答案和解析>>
科目:初中数学 来源: 题型:
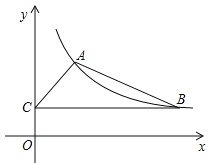
【题目】如图,某反比例函数图象的一支经过点A(2,3)和点B(点B在点A的右侧),作BC⊥y轴,垂足为点C,连结AB,AC.
(1)求该反比例函数的解析式;
(2)若△ABC的面积为6,求直线AB的表达式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com