
���� ��1����P��������뼴����������������Ľ���ʽ����ֱ�߽���ʽΪy=ax+b����P��2��3������ó�y=kx+3-2k������ֱ���뷴��������ʽ�ó�����kx2+��3-2k��x-6=0�����ݸ���ϵ���Ĺ�ϵ���k���������ֱ�ߵĽ���ʽ��
��2���ɣ�1�������ֱ��y=-$\frac{3}{2}$x+6�����A��B�����꣬�ó�OA=4��OB=6����ֱ��CD�Ľ���ʽΪy=mx+n���ɵ�$\left\{\begin{array}{l}{y=mx+n}\\{y=\frac{6}{x}}\end{array}\right.$ֻ��һ���⣬�̶�֤��$\frac{OA}{OC}=\frac{OD}{OB}$�����֤�ý��ۣ�
��3����OC=t����OD=$\frac{24}{t}$������S�ı���ABCD=S��BCD+S��BDA�ó�S=3t+$\frac{48}{t}$+24�����ɶ���ʽ�������t���������ε��ж��Ƴ����ɣ�
��� 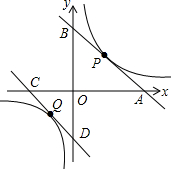 ��1���⣺��P��������뷴��������ʽ�ã�3=$\frac{k}{2}$����k=6��
��1���⣺��P��������뷴��������ʽ�ã�3=$\frac{k}{2}$����k=6��
������������ʽΪy=$\frac{6}{x}$��
��ֱ�߽���ʽΪy=ax+b��
�߰�P��2��3������ã�3=2k+b��
��b=3-2k��
��y=kx+3-2k��
����ֱ���뷴��������ʽ�ã�
$\left\{\begin{array}{l}{y=kx+3-2k}\\{y=\frac{6}{x}}\end{array}\right.$��
��ȥy�����ã�kx2+��3-2k��x-6=0��
������õ�������������ȵ�ʵ�������õ���=��3-2k��2+24k=9-12k+4k2+24k=9+12k+4k2=��2k+3��2=0��
��ã�k=-$\frac{3}{2}$��
��ֱ��Ϊ��y=-$\frac{3}{2}$x+6��
��2��AD��BC�����ɣ�֤�����ɣ�1�������ֱ��y=-$\frac{3}{2}$x+6����x=0���õ�y=6����y=0���õ�x=4��
��A��4��0����B��0��6������OA=4��OB=6��
��ֱ��CD�Ľ���ʽΪy=mx+n��
��$\left\{\begin{array}{l}{y=mx+n}\\{y=\frac{6}{x}}\end{array}\right.$ֻ��һ���⣬
��ȥy�����ã�mx2+nx-6=0��
��=n2+24m=0��
-$\frac{{n}^{2}}{m}$=24��
OC•OD=$\frac{n}{m}$•��-n��=24=OA•OB����$\frac{OA}{OC}=\frac{OD}{OB}$��
��AD��BC��
��3���ı���ABCDΪ���Σ����ɣ�֤������OC=t����OD=$\frac{24}{t}$��
S�ı���ABCD=S��BCD+S��BDA=$\frac{1}{2}$����6+$\frac{24}{t}$����t+$\frac{1}{2}$����6+$\frac{24}{t}$����4
=3t+$\frac{48}{t}$+24
=3��$\sqrt{t}$-$\frac{4}{\sqrt{t}}$��2+48��
��$\sqrt{t}$-$\frac{4}{\sqrt{t}}$=0����t=4ʱ���ı���ABCD�����С��
��ʱOA=OC=4��OB=OD=6��
�֡�AC��BD��
���ı���ABCDΪ���Σ�
���� �������ڷ����������ۺ��⣮�����˷��������������ʡ����ε��ж���ƽ���ߵ��ж��Լ���ֵ���⣮ע������һԪ���η��̸���������ж�����������ǽ����Ĺؼ���


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
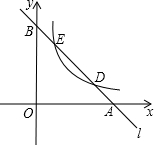 ��ֱ֪��l�ֱ���x�ᡢy�ύ��A��B���㣬��˫����y=$\frac{a}{x}$��a��0��x��0���ֱ���D��E���㣮����D������Ϊ��3��1������E������Ϊ��1��n��
��ֱ֪��l�ֱ���x�ᡢy�ύ��A��B���㣬��˫����y=$\frac{a}{x}$��a��0��x��0���ֱ���D��E���㣮����D������Ϊ��3��1������E������Ϊ��1��n���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
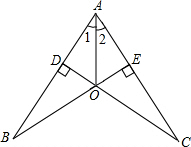 ��ͼ��CD��AB��BE��AC������ֱ�ΪD��E��BE��CD���ڵ�O��OB=OC����֤����1=��2��
��ͼ��CD��AB��BE��AC������ֱ�ΪD��E��BE��CD���ڵ�O��OB=OC����֤����1=��2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com