
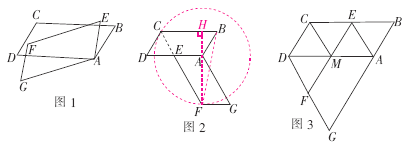
【题目】如图1, ![]() ABCD和
ABCD和![]() AEFG是两个能完全重合的平行四边形,现从AB与AE重合时开始,将
AEFG是两个能完全重合的平行四边形,现从AB与AE重合时开始,将![]() ABCD固定不动,
ABCD固定不动, ![]() AEFG绕点A逆时针旋转,旋转角为α(0°<α<360°),AB=a,BC=2a;并发现:如图2,当
AEFG绕点A逆时针旋转,旋转角为α(0°<α<360°),AB=a,BC=2a;并发现:如图2,当![]() AEFG旋转到点E落在AD上时,FE的延长线恰好通过点C.
AEFG旋转到点E落在AD上时,FE的延长线恰好通过点C.
探究一:
(1)在图2的情形下,求旋转角α的度数;
探究二:
(2)如图3,当![]() AEFG旋转到点E落在BC上时,EF与AD相交于点M,连接CM,DF,请你判断四边形CDFM的形状,并给予证明;
AEFG旋转到点E落在BC上时,EF与AD相交于点M,连接CM,DF,请你判断四边形CDFM的形状,并给予证明;
探究三:
(3)如图1,连接CF,BF,在旋转过程中△BCF的面积是否存在最大的情形,如果存在,求出最大面积,如果不存在,请说明理由.
【答案】(1)α=120°;(2)四边形CDFM是菱形,证明见解析;(3)存在△BCF的面积最大的情形,S△BCF =![]() a2.
a2.
【解析】试题分析:(1)由平行四边形的性质知
∠D=∠B,AB=CD=a,可得∠D=∠DEC,由等角对等边知CD=CE,由AE=AB=a,AD=BC=2a,可得DE=CE,即可证得△CDE是等边三角形,∠D=60°,由两直线平行,同位角相等可得∠DAB=120°,即可求得α;
(2)由旋转的性质以及∠B=60°,可得△ABE是等边三角形,由平行线的判定以及两组对边分别平行的四边形是平行四边形可证四边形ABEM是平行四边形,再由由一组邻边相等的平行四边形是菱形即可得证;
(3)当点F到BC的距离最大时,△BCF的面积最大,由于点F始终在以A为圆心AF为半径的圆上运动,故当FG与⊙A相切时,点F到BC的距离最大,过点A作AH⊥BC于点H,连接AF,由题意知∠AFG=90°.由∠ABH=∠G=60°,AB=a,AG=2a,可得AH、AF的值.可求得点F到BC的最大距离.进而求得S△BCF的值.
试题解析:(1)∵四边形ABCD是平行四边形,
∴∠D=∠B,AB=CD=a,
∵∠AEF=∠B,∠AEF=∠DEC,
∴∠D=∠DEC,
∴CD=CE,
∵AE=AB=a,AD=BC=2a,
∴DE=CE.,
∴CD=CE=DE,
∴△CDE是等边三角形,
∴∠D=60°,
∵CD∥AB,
∴∠D+∠DAB=180°,
∴∠DAB=120°,
∴α=120°.;
(2)四边形CDFM是菱形.
证明:由旋转可得AB=AE,
∵∠B=60°,
∴△ABE是等边三角形,
∴∠BAE=60°,
∴∠BAG=∠BAE+∠GAE=60°+120°=180°,
∴点G,A,B在同一条直线上,
∴ME ∥AB,BE∥AM,
∴四边形ABEM是平行四边形,
∴AM=AB=ME,
∴CD=DM=MF,
∵CD ∥AB∥MF,
∴四边形CDFM是平行四边形,
∵∠D= 60°,CD=DM,
∴△CDM是等边三角形,
∴CD=DM,
∴四边形CDFM是菱形;
(3)存在△BCF的面积最大的情形.
∵CB的长度不变,
∴当点F到BC的距离最大时,△BCF的面积最大.
∵点F始终在以A为圆心AF为半径的圆上运动,
∴当FG与⊙A相切时,点F到BC的距离最大,
如图,过点A作AH⊥BC于点H,连接AF,
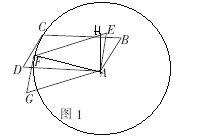
则∠AFG=90°.
∵∠ABH=∠G=60°,AB=a,AG=2a,
∴AH=AB×sin60°=![]() a,AF=AG×sin60°=
a,AF=AG×sin60°=![]() a.
a.
∴点F到BC的最大距离为![]() a+
a+ ![]() a=
a=![]() a.
a.
∴S△BCF=![]() ×2a×
×2a×![]() a=
a=![]() a2.
a2.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】张明暑假期间参加社会实践活动,从某批发市场以批发价每个m元的价格购进100个手机充电宝,然后每个加价n元到市场出售.
(1)求售出100个手机充电宝的总售价为多少元(结果用含m,n的式子表示)?
(2)由于开学临近,张明在成功售出60个充电宝后,决定将剩余充电宝按售价8折出售,并很快全部售完.
①她的总销售额是多少元?
②相比不采取降价销售,她将比实际销售多盈利多少元(结果用含m、n的式子表示)?
③若m=2n,张明实际销售完这批充电宝的利润率为 (利润率=利润÷进价×100%)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从背面相同的同一副扑克牌中取出红桃9张、黑桃10张、方块11张,现将这些牌洗匀背面朝上放在桌面上.
(1)求从中抽出一张牌是红桃的概率;
(2)现从桌面上先抽掉若干张黑桃,再放入与抽掉的黑桃张数相同的红桃,并洗匀且背面都朝上排开后,随机抽一张是红桃的概率不小于![]() ,问至少抽掉了多少张黑桃?
,问至少抽掉了多少张黑桃?
(3)若先从桌面上抽掉9张红桃和m(m>6)张黑桃后,再在桌面抽出一张牌.
①当m为何值时,事件“再抽出的这张牌是方块”为必然事件?
②当m为何值时,事件“再抽出的这张牌是方块”为随机事件?并求出这个事件的概率的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某检修小组乘汽车从![]() 地出发,在东西走向的马路上检修线路,如果规定向东行驶为正,一天中七个检修点的行驶记录如下(单位:
地出发,在东西走向的马路上检修线路,如果规定向东行驶为正,一天中七个检修点的行驶记录如下(单位:![]() ):
):
-4,+7,-9,+8,+6,-4,-3.
(1)收工时汽车共行驶了多少千米?
(2)收工时,汽车距![]() 地多远?
地多远?
(3)在检修时,第几个检修点离![]() 地最远,最远距离是多少?
地最远,最远距离是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题14分)如图(1),在△ABC和△EDC中,D为△ABC边AC上一点,CA平分∠BCE,BC=CD,AC=CE.


(1)求证:△ABC≌△EDC;
(2)如图(2),若∠ACB=60°,连接BE交AC于F,G为边CE上一点,满足CG=CF,连接DG交BE于H.
①求∠DHF的度数;
②若EB平分∠DEC,试说明:BE平分∠ABC.
查看答案和解析>>
科目:初中数学 来源: 题型:
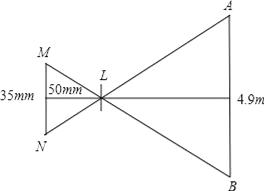
【题目】如图,是一个照相机成像的示意图,像高MN,景物高度AB、
CD为水平视线,根据物体成像原理知:AB∥MN,CD⊥MN.
(1)如果像高MN是35mm,焦距CL是50mm,拍摄的景物高度AB是4.9m,拍摄点离景物的距离LD是多少?
(2)如果要完整的拍摄高度是2m的景物,拍摄点离景物有4m,像高不变,则相机的焦距应调整为多少毫米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工程,由甲、乙两队承包,![]() 天可以完成,需支付1800元;由乙、丙两队承包,
天可以完成,需支付1800元;由乙、丙两队承包,![]() 天可以完成,需支付1500元;由甲、丙两队承包,
天可以完成,需支付1500元;由甲、丙两队承包,![]() 天可以完成,需支付1600元.在保证一星期内完成的前提下,选择哪个队单独承包费用最少?
天可以完成,需支付1600元.在保证一星期内完成的前提下,选择哪个队单独承包费用最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题呈现:我们知道反比例函数y=![]() (x>0)的图象是双曲线,那么函数y=
(x>0)的图象是双曲线,那么函数y=![]() +n(k、m、n为常数且k≠0)的图象还是双曲线吗?它与反比例函数y=
+n(k、m、n为常数且k≠0)的图象还是双曲线吗?它与反比例函数y=![]() (x>0)的图象有怎样的关系呢?让我们一起开启探索之旅……
(x>0)的图象有怎样的关系呢?让我们一起开启探索之旅……
探索思考:我们可以借鉴以前研究函数的方法,首先探索函数y=![]() 的图象.
的图象.
(1)填写下表,并画出函数y=![]() 的图象.
的图象.
①列表:
x | … | ﹣5 | ﹣3 | ﹣2 | 0 | 1 | 3 | … |
y | … | … |
②描点并连线.
(2)观察图象,写出该函数图象的两条不同类型的特征:
① ② ;
理解运用:函数y=![]() 的图象是由函数y=
的图象是由函数y=![]() 的图象向 平移 个单位,其对称中心的坐标为 .
的图象向 平移 个单位,其对称中心的坐标为 .
灵活应用:根据上述画函数图象的经验,想一想函数y=![]() +2的图象大致位置,并根据图象指出,当x满足 时,y≥3.
+2的图象大致位置,并根据图象指出,当x满足 时,y≥3.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com