
【题目】某工程,由甲、乙两队承包,![]() 天可以完成,需支付1800元;由乙、丙两队承包,
天可以完成,需支付1800元;由乙、丙两队承包,![]() 天可以完成,需支付1500元;由甲、丙两队承包,
天可以完成,需支付1500元;由甲、丙两队承包,![]() 天可以完成,需支付1600元.在保证一星期内完成的前提下,选择哪个队单独承包费用最少?
天可以完成,需支付1600元.在保证一星期内完成的前提下,选择哪个队单独承包费用最少?
【答案】选择乙来做,在![]() 天完工,且只用
天完工,且只用![]() 元.
元.
【解析】
根据题意,我们应该计算出甲乙丙三队单独完成工程时所用的时间和费用,再选择在保证一星期内完成的前提下,且费用最少的队.
题目条件告诉了我们甲乙丙两两合作所需的时间和费用,把工程看作单位“1”,通过这三个条件分别算出三队两两合作的工作效率和工作一天的费用.然后算出甲乙丙三人一起合作的工作效率和工作一天费用,再通过三人合作的工作效率-两两合作的工作效率=单组的工作效率,同理得到单组每天的费用.
甲乙合作一天完成![]() ,支付
,支付![]() 元
元
乙丙合作一天完成![]() ,支付
,支付![]() 元
元
甲丙合作一天完成![]() ,支付
,支付![]() 元
元
三人合作一天完成![]() ,
,
三人合作一天支付![]() 元
元
甲单独做每天完成![]() ,支付
,支付![]() 元
元
乙单独做每天完成![]() ,支付
,支付![]() 元
元
丙单独做每天完成![]() ,支付
,支付![]() 元
元
所以通过比较:选择乙来做,在![]() 天完工,且只用
天完工,且只用![]() 元
元


科目:初中数学 来源: 题型:
【题目】端午节快到了,小明准备买粽子过节,若在超市购买![]() 盒甲品牌粽子和
盒甲品牌粽子和![]() 盒乙品牌粽子需支付
盒乙品牌粽子需支付![]() 元,而在某团购群购买
元,而在某团购群购买![]() 盒甲品牌粽子和
盒甲品牌粽子和![]() 盒乙品牌粽子需支付
盒乙品牌粽子需支付![]() 元对比发现,甲品牌粽子每盒的团购价相当于超市价的八折,乙品牌粽子每盒的团购价相当于超市价的七五折
元对比发现,甲品牌粽子每盒的团购价相当于超市价的八折,乙品牌粽子每盒的团购价相当于超市价的七五折
(1)甲、乙两种品牌粽子每盒的超市价分别是多少元?
(2)若购买甲品牌粽子![]() 盒,乙品牌粽子
盒,乙品牌粽子![]() 盒,则在团购群购买比在超市购买能省多少钱?
盒,则在团购群购买比在超市购买能省多少钱?
(3)小明要打算在团购群购买这两种品牌的粽子,其中乙品牌粽子比甲品牌粽子多![]() 盒,总花费不超过
盒,总花费不超过![]() 元,问小明最多能买多少盒甲品牌粽子?
元,问小明最多能买多少盒甲品牌粽子?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1, ![]() ABCD和
ABCD和![]() AEFG是两个能完全重合的平行四边形,现从AB与AE重合时开始,将
AEFG是两个能完全重合的平行四边形,现从AB与AE重合时开始,将![]() ABCD固定不动,
ABCD固定不动, ![]() AEFG绕点A逆时针旋转,旋转角为α(0°<α<360°),AB=a,BC=2a;并发现:如图2,当
AEFG绕点A逆时针旋转,旋转角为α(0°<α<360°),AB=a,BC=2a;并发现:如图2,当![]() AEFG旋转到点E落在AD上时,FE的延长线恰好通过点C.
AEFG旋转到点E落在AD上时,FE的延长线恰好通过点C.
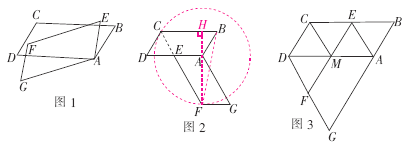
探究一:
(1)在图2的情形下,求旋转角α的度数;
探究二:
(2)如图3,当![]() AEFG旋转到点E落在BC上时,EF与AD相交于点M,连接CM,DF,请你判断四边形CDFM的形状,并给予证明;
AEFG旋转到点E落在BC上时,EF与AD相交于点M,连接CM,DF,请你判断四边形CDFM的形状,并给予证明;
探究三:
(3)如图1,连接CF,BF,在旋转过程中△BCF的面积是否存在最大的情形,如果存在,求出最大面积,如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了调查学生对“节约教育”内容的了解程度(程度分为:“![]() —了解很多”,“
—了解很多”,“![]() —了解较多”,“
—了解较多”,“![]() —了解较少”,“
—了解较少”,“![]() —不了解”),对某中学的部分学生进行了调查,将这次调查的结果绘制成以下两幅统计图.根据以上信息,解答下列问顾:
—不了解”),对某中学的部分学生进行了调查,将这次调查的结果绘制成以下两幅统计图.根据以上信息,解答下列问顾:
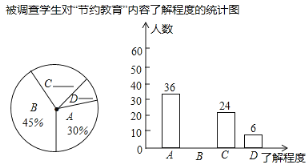
(1)本次调查了多少名学生?
(2)若该校共有1800名学生,请你估计这所学校的所有学生中,对“节约教育”内容“了解较多”的有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形OABC的两条边在坐标轴上,OA=1,OC=2,现将此矩形向右平移,每次平移1个单位,若第1次平移得到的矩形的边与反比例函数图象有两个交点,它们的纵坐标之差的绝对值为0.6,则第n次(n>1)平移得到的矩形的边与该反比例函数图象的两个交点的纵坐标之差的绝对值为________(用含n的代数式表示).
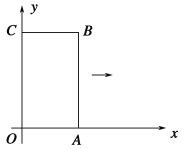
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=90°,AB=6,BC=8,将△ABC沿DE折叠,使点C落在AB边上的点F处,并且FD∥BC,则CD的长是( )
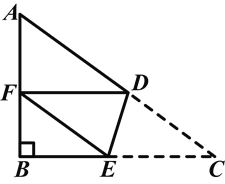
A. ![]()
B. ![]()
C. ![]()
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,钟表的分针匀速旋转一周需要60分钟,那么:
(1)它的旋转中心是什么?
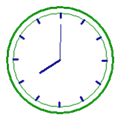
(2)分针旋转一周,时针旋转多少度?
(3)上午8点整,时针和分针的夹角是多少?8点半呢?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是坐标原点,矩形OABC的顶点A,C分别在坐标轴上,点B的坐标为(4,2).直线![]() 分别交AB,BC于点M,N,反比例函数
分别交AB,BC于点M,N,反比例函数![]() 的图像经过点M.
的图像经过点M.
(1)求反比例函数的解析式;
(2)判断点N是否在反比例函数![]() 的图像上?试说明理由.
的图像上?试说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】倡导健康生活,推进全民健身,某社区要购进A,B两种型号的健身器材若干套,A,B两种型号健身器材的购买单价分别为每套310元,460元,且每种型号健身器材必须整套购买.
(1)若购买A,B两种型号的健身器材共50套,且恰好支出20000元,求A,B两种型号健身器材各购买多少套?
(2)若购买A,B两种型号的健身器材共50套,且支出不超过18000元,求A种型号健身器材至少要购买多少套?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com