
����Ŀ�����ϣ�һ��أ�n����ͬ������a��ˣ� 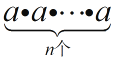 ��Ϊan ��
��Ϊan ��
��23=8����ʱ��3������2Ϊ��8�Ķ�������Ϊlog28����log28=3����
һ��أ���an=b��a��0��a��1��b��0������n������aΪ��b�Ķ�������Ϊlogab����logab=n������34=81����4������3Ϊ��81�Ķ�������Ϊlog381����log381=4����
���⣺
��1��log24��log216��log264֮������ĵ�����ϵ����
��2���²���ۣ�logaM+logaN=��a��0��a��1��M��0��N��0��
��3�������ݵ����㷨��anam=an+m�Լ������ĺ���˵����2������ó��Ľ��ۣ�
���𰸡�
��1��log24+log216=log264
��2��logaMN
��3��
�⣺��x=logaM��y=logaN��
���ݶ����ĺ��壺ax=M��ay=N��
�����ݵ����㷨��MN=axay=ax+y��
���ݶ����ĺ��壺x+y=logaMN��
��logaM+logaN=x+y=logaMN.
����������1��log24=2��log216=4��log264=6����log24+log216=log264����2���ɣ�1�����У�log24+log216=log2��4��16��=log264���ɲ²�logaM+logaN=x+y=logaMN.
�����㾫�����������⣬������Ҫ�˽�����ʽ�Ĺ���(�ȴ�ͼ����Ѱ�ҹ��ɣ�Ȼ����֤���ɣ�Ӧ�ù��ɣ������ν��Ѱ�ҹ���)����Ҫ����ͬ�����ݵij˷�(ͬ�����ݵij˷�����aman=am+n(m,n��������))�����֪ʶ���Ǵ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������У���ȷ���ǣ�������
A.2a��a��1B.a+a��2aC.��a3��3��a6D.a8��a2��a4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̵깺������������Ʒ���Ľ������۱��ҵĽ������۸�20Ԫ����֪20������Ʒ�Ľ����ܼ���25������Ʒ�Ľ����ܼ���ͬ��
��1����ס���ÿ����Ʒ�Ľ������ۣ�
��2�����ס���������Ʒ������100����Ҫ��������Ʒ�Ľ����ܼ۲�����9000Ԫ��ͬʱ����Ʒ���������10%��ļ۸����ۣ�����Ʒ���������25%��ļ۸����ۣ�������Ʒȫ�������������ܶ����10480Ԫ�������ļ��ֽ���������
��3����������2���£����Ҳ��ٿ����������أ�������������Ʒȫ�����꣬���ַ������������������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������1+6+62+63+64+65+66+67+68+69��ֵʱ��С�ַ��֣��ӵڶ���������ÿһ����������ǰһ��������6�����������裺
S=1+6+62+63+64+65+66+67+68+69��
Ȼ���ڢ�ʽ�����߶�����6���ã�
6S=6+62+63+64+65+66+67+68+69+610��
�ک��ٵ�6S��S=610��1����5S=610��1��
����S= ![]() ��
��
�ó��𰸺����Խ��С���룺����ѡ�6��������ĸ��a����a��0��a��1�����ܷ����1+a+a2+a3+a4+��+a2014��ֵ����Ĵ��ǣ�������
A.![]()
B.![]()
C.![]()
D.a2015��1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ۺ��⡣
��1�����㣺��14��16�£���2��3+|�� ![]() |����1��0.5��
|����1��0.5��
��2������4xy��3y2��3x2+xy��3xy��2x2��4y2 ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̵����һ������ÿ��3Ԫ������ʱÿ���Ӽ�0.5Ԫ�����۳�x��Ӧ�������yԪ����ôy(Ԫ)��x(��)�ĺ�������ʽ��_________________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����䷽���Ѷ��κ���y=x2+4x��5����y=a��x��h��2+k����ʽ��д���������꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ߣ��DZ���������ɽ�ߵ������ߣ������ڽ���ʩ����ͨ�������й���½�ڶ���ȫ�Զ����˼�ʻ��·��Ԥ����ڿ������վ�132300�˴Σ���132300�ÿ�ѧ��������ʾΪ( )
A.1.323��105B.1.323��104C.1.3��105D.1.323��106
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com