练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，△ABC是等边三角形，D是AB边上一点，以CD为边作等边三角形CDE，使点E，A在直线DC的同侧，连接AE．求证：AE∥BC．


    ∵△ABC和△EDC是等边三角形，∴∠BCA=∠DCE=160°，BC=AC，DC=EC．∴∠BCA－∠ACD=∠DCE－∠ACD，即∠BCD=∠ACE．∴△DBC≌△EAC (SAS)．∴∠DBC=∠EAC．又∵∠DBC=∠ACB=60°，∴∠ACB=∠EAC．∴AE∥BC．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


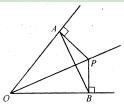
    如图，OP平分∠AOB，PA⊥OA，PB⊥OB，垂足分别为A，B．下列结论中不一定成立的是    (    )

       A．PA=PB    B．PO平分∠APB    C．OA=OB    D．AB垂直平分OP

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    若a，b，c是三角形的三条边，且满足a2+ac=ab+bc，则该三角形的形状为．    (    )

       A．等腰三角形    B．等边三角形    C．等腰直角三角形    D．钝角三角形

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在等边三角形ABC中，中线AD，BE相交于点O，图中的等腰三角形有    (    )

       A．3个       B．4个        C．5个      D．6个

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在等边△ABC中，AC=9，点O在AC上，且AO=3，点P是AB上一动点，连接OP，将线段OP绕点O逆时针旋转60°得到线段OD．要使点D恰好落在BC上，则AP的长为        ．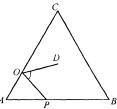

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    据教育部通报，2014年参加全国硕士研究生入学考试的人数约为1720000． 数字1720000用科学记数法表示为（    ）

    A、17.2×105　　　　B、1.72×106　　　C、1.72×105　　　D、0.172×107

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    一个多边形的内角和是720°，这个多边形的边数是　　      ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    【试题再现】如图1，Rt△ABC中，∠ACB＝90°，AC＝BC，直线l过点C，过点A，B分别作AD⊥l于点D，BE⊥l于点E，则DE＝AD＋BE（不用证明）.

    （1）【类比探究】如图2，在△ABC中，AC＝BC，且∠ACB＝∠ADC＝∠BEC＝100°，上述结论是否成立？若成立，请说明理由；若不成立，请写出一个你认为正确的结论.

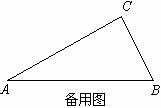
    （2）【拓展延伸】①如图3，在△ABC中，AC＝nBC，且∠ACB＝∠ADC＝∠BEC＝100°，猜想线段DE、AD、BE之间有什么数量关系？并证明你的猜想.

    ②若图1的Rt△ABC中，∠ACB＝90°，AC＝nBC，并将直线l绕点C旋转一定角度后与斜边AB相交，分别过点A、B作直线l的垂线，垂足分别为点D和点E，请画出图形，并直接写出线段DE、AD、BE之间满足的一种数量关系（不要求写出证明过程）.

    　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，⊙O的弦AB＝6，M是AB上任意一点，且OM的最小值为4，则⊙O的半径为 (   )   ．5  ．4    ．3  　．2

     


    查看答案和解析>>

    同步练习册答案