【题目】如图，线段AB是直线y=4x+2的一部分，点A是直线与y轴的交点，点B的纵坐标为6，曲线BC是双曲线y=
的一部分，点C的横坐标为6，由点C开始不断重复“A﹣B﹣C”的过程，形成一组波浪线．点P（2017，m）与Q（2020，n）均在该波浪线上，分别过P、Q两点向x轴作垂线段，垂足为点D和E，则四边形PDEQ的面积是（ ）
A. 10 B. 
C. 
D. 15
科目：初中数学 来源： 题型：
【题目】某店只销售某种进价为40元/kg的产品，已知该店按60元kg出售时，每天可售出100kg，后来经过市场调查发现，单价每降低1元，则每天的销售量可增加10kg．
（1）若单价降低2元，则每天的销售量是_____千克，每天的利润为_____元；若单价降低x元，则每天的销售量是_____千克，每天的利润为______元；（用含x的代数式表示）
（2）若该店销售这种产品计划每天获利2240元，单价应降价多少元？
（3）当单价降低多少元时，该店每天的利润最大，最大利润是多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】二次函数y=ax2+bx+c（a≠0）图象如图，下列结论：
①abc＞0；②3a+c＜0；③a+b≥am2+bm；④a﹣b+c＞0；⑤若ax12+bx1=ax22+bx2，且x1≠x2，则x1+x2=2．
其中正确的有（ ）个．
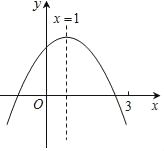
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知一元二次方程2x2+2x﹣1=0的两个根为x1，x2，且x1＜x2，下列结论正确的是（ ）
A. x1+x2=1 B. x1x2=﹣1 C. |x1|＜|x2| D. x12+x1=
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，菱形OABC的一边OA在x轴的负半轴上，O是坐标原点，tan∠AOC=
，反比例函数y=
的图象经过点C，与AB交于点D，若△COD的面积为20，则k的值等于_____．
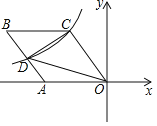
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知△ABC中，∠ACB=90°，AC=BC=2，将直角边AC绕A点逆时针旋转至AC′，连接BC′，E为BC′的中点，连接CE,则CE的最大值为( ).
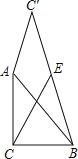
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】问题探究：已知平行四边形
的面积为
，
是
所在直线上一点．
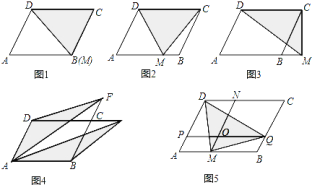
如图
：当点与
重合时，
________；
如图
，当点与与
均不重合时，________；
如图
，当点在（或
）的延长线时，________．
拓展推广：如图
，平行四边形的面积为
，
、
分别为
、
延长线上两点，连接
、
、
、
，求出图中阴影部分的面积，并说明理由．
实践应用：如图是一平行四边形绿地，
、
分别平行于、
，它们相交于点
，
，
，
，
，现进行绿地改造，在绿地内部作一个三角形区域
（连接
、
、
，图中阴影部分）种植不同的花草，求出三角形区域的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
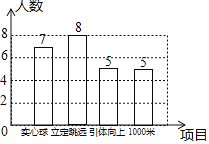
【题目】某学校为了了解男生的体能情况，规定参加测试的每名男生从“实心球”，“立定跳远”，“引体向上”，“耐久跑1000米”四个项目中随机抽取一项作为测试项目．
（1）八年（1）班的25名男生积极参加，参加各项测试项目的统计结果如图，参加“实心球”测试的男生人数是 人；
（2）八年（1）班有8名男生参加了“立定跳远”的测试，他们的成绩（单位：分）如下：95，100，82，90，89，90，90，85
①“95，100，82，90，89，90，90，85”这组数据的众数是 ，中位数是 ．
②小聪同学的成绩是92分，他的成绩如何？
③如果将不低于90分的成绩评为优秀，请你估计八年级80名男生中“立定跳远”成绩为优秀的学生约为多少人？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
