
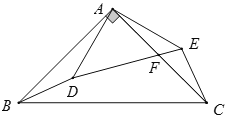
【题目】如图,在△ABC中,∠BAC=90°,AB=AC=10cm,点D为△ABC内一点,∠BAD=15°,AD=6cm,连接BD,将△ABD绕点A逆时针方向旋转,使AB与AC重合,点D的对应点E,连接DE,DE交AC于点F,则CF的长为________cm.
【答案】![]()
【解析】
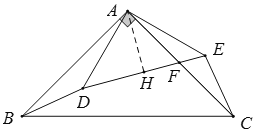
过点A作AH⊥DE,垂足为H,由旋转的性质可得 AE=AD=6,∠CAE=∠BAD=15°,∠DAE=∠BAC=90°,再根据等腰直角三角形的性质可得∠HAE=45°,AH=3![]() ,进而得∠HAF=30°,继而求出AF长即可求得答案.
,进而得∠HAF=30°,继而求出AF长即可求得答案.
过点A作AH⊥DE,垂足为H,
∵∠BAC=90°,AB=AC,将△ABD绕点A逆时针方向旋转,使AB与AC重合,点D的对应点E,
∴AE=AD=6,∠CAE=∠BAD=15°,∠DAE=∠BAC=90°,
∴DE=![]() ,∠HAE=
,∠HAE=![]() ∠DAE=45°,
∠DAE=45°,
∴AH=![]() DE=3
DE=3![]() ,∠HAF=∠HAE-∠CAE=30°,
,∠HAF=∠HAE-∠CAE=30°,
∴AF=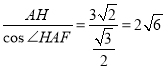 ,
,
∴CF=AC-AF=![]() ,
,
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】在初中阶段的函数学习中,我们经历了“确定函数的表达式﹣利用函数图象研究其性质﹣应用函数解决问题”的学习过程.在画函数图象时,我们通过描点或平移的方法画出了一个陌生函数的大致图象,结合上面经历的学习过程,现在来解决下面问题:在函数y=![]() 中,当x=0时,y=1;当x=2时,y=
中,当x=0时,y=1;当x=2时,y=![]() .
.
(1)求这函数的表达式 ;
(2)在给出的平面直角坐标系中画出这个函数的大致图象并写出这个函数的一条性质 ;
(3)结合你所画的函数图象与y=![]() x+
x+![]() 的图象,直接写出不等式组
的图象,直接写出不等式组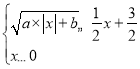 的解集.
的解集.
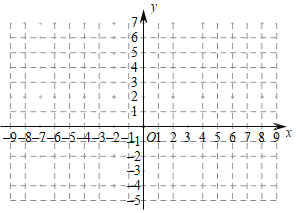
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中有![]() ,
,![]() 为原点,
为原点,![]() ,
,![]() ,将此三角形绕点
,将此三角形绕点![]() 顺时针旋转
顺时针旋转![]() 得到
得到![]() ,抛物线
,抛物线![]()
![]() 过
过![]() 三点.
三点.
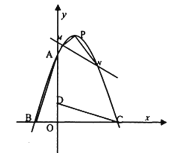
(1)求此抛物线的解析式及顶点![]() 的坐标;
的坐标;
(2)直线![]() 与抛物线交于
与抛物线交于![]() 两点,若
两点,若![]() ,求
,求![]() 的值;
的值;
(3)抛物线的对称轴上是否存在一点![]() 使得
使得![]() 为直角三角形.
为直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2﹣bx+2b(b是常数).
(1)无论b取何值,该抛物线都经过定点 D.请写出点D的坐标.
(2)该抛物线的顶点是(m,n),当b取不同的值时,求n关于m的函数解析式.
(3)若在0≤x≤4的范围内,至少存在一个x的值,使y<0,求b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
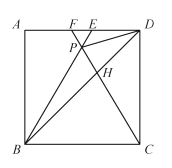
【题目】如图,在正方形![]() 中,
中,![]() 是等边三角形,
是等边三角形,![]() 的延长线分别交
的延长线分别交![]() 于点
于点![]() ,连结
,连结![]() 与
与![]() 相交于点H.给出下列结论,
相交于点H.给出下列结论,
①△ABE≌△DCF;②△DPH是等腰三角形;③![]() ;④
;④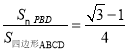 ,
,
其中正确结论的个数是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
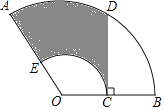
【题目】如图,扇形OAB中,∠AOB=100°,OA=12,C是OB的中点,CD⊥OB交![]() 于点D,以OC为半径的
于点D,以OC为半径的![]() 交OA于点E,则图中阴影部分的面积是( )
交OA于点E,则图中阴影部分的面积是( )
A. 12π+18![]() B. 12π+36
B. 12π+36![]() C. 6π+18
C. 6π+18![]() D. 6π+36
D. 6π+36![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com