
【题目】在平面直角坐标系中有![]() ,
,![]() 为原点,
为原点,![]() ,
,![]() ,将此三角形绕点
,将此三角形绕点![]() 顺时针旋转
顺时针旋转![]() 得到
得到![]() ,抛物线
,抛物线![]()
![]() 过
过![]() 三点.
三点.
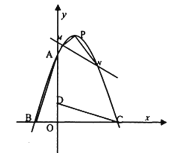
(1)求此抛物线的解析式及顶点![]() 的坐标;
的坐标;
(2)直线![]() 与抛物线交于
与抛物线交于![]() 两点,若
两点,若![]() ,求
,求![]() 的值;
的值;
(3)抛物线的对称轴上是否存在一点![]() 使得
使得![]() 为直角三角形.
为直角三角形.
【答案】(1)![]() ;点
;点![]() ;(2)
;(2)![]() ;(3)存在,Q1(1,-1),Q2(1,2), Q3(1,4), Q4(1,-5).
;(3)存在,Q1(1,-1),Q2(1,2), Q3(1,4), Q4(1,-5).
【解析】
(1)用待定系数法可求抛物线的解析式,进行配成顶点式即可写出顶点坐标;
(2)将直线与抛物线联立,通过根与系数关系得到![]() ,
,![]() ,再通过
,再通过![]() 得出
得出![]() ,通过变形得出
,通过变形得出![]() 代入即可求出
代入即可求出![]() 的值;
的值;
(3)分:![]() ,
, ![]() ,
, ![]() 三种情况分别利用勾股定理进行讨论即可.
三种情况分别利用勾股定理进行讨论即可.
(1)∵![]() ,
,![]() ,
,
![]()
∵![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,得到
,得到![]() ,
,
![]()
∴点![]() 的坐标为:
的坐标为:![]() ,
,
将点A,B代入抛物线![]() 中得
中得
![]() 解得
解得![]()
∴此抛物线的解析式为:![]()
∵![]() ;
;
∴点![]()
(2)直线![]() :
:![]() 与抛物线的对称轴交点
与抛物线的对称轴交点![]() 的坐标为
的坐标为![]() ,
,
交抛物线于![]() ,
,![]() ,
,![]()
由![]() 得:
得:![]()
∴![]() ,
,![]()
∵![]() ,
,
∴![]()
∴![]()
∴![]()
∴![]()
∴![]()

(3)存在,![]() 或
或![]() ,
,![]() ,
,![]()
![]()
∴![]()
设点![]()
![]() ,
,![]()
若![]() ,则
,则![]()
即![]()
∴![]() 或
或![]()
若![]() ,则
,则![]()
即![]()
∴![]()
若![]() ,则
,则![]()
即![]()
∴![]()
即Q1(1,-1), Q2(1,2), Q3(1,4), Q4(1,-5).


科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx﹣3与x轴交于A,B两点,与y轴交于点C,且OB=OC=3OA,求抛物线的解析式( )
A.y=x2﹣2x﹣3B.y=x2﹣2x+3C.y=x2﹣2x﹣4D.y=x2﹣2x﹣5
查看答案和解析>>
科目:初中数学 来源: 题型:
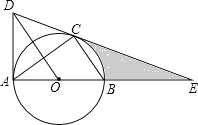
【题目】如图,⊙O是△ABC的外接圆,AB是直径,作OD∥BC与过点A的切线交于点D,连接DC并延长交AB的延长线于点E.
(1)求证:DE是⊙O的切线;
(2)若AE=6,CE=2![]() ,求线段CE、BE与劣弧BC所围成的图形面积.(结果保留根号和π)
,求线段CE、BE与劣弧BC所围成的图形面积.(结果保留根号和π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在今年“绿色清明,文明祭祀”活动中,某花店用![]() 元购进若干菊花,很快售完,接着又用
元购进若干菊花,很快售完,接着又用![]() 元购进第二批菊花,已知第二批所购进菊花的数量是第一批所购进菊花数量的
元购进第二批菊花,已知第二批所购进菊花的数量是第一批所购进菊花数量的![]() 倍,且每朵菊花的进价比第一批每朵菊花的进价多
倍,且每朵菊花的进价比第一批每朵菊花的进价多![]() 元.
元.
(1)求第一批每朵瓶菊花的进价是多少元?
(2)若第一批每朵菊花按![]() 元售价销售,要使总利润不低于
元售价销售,要使总利润不低于![]() 元(不考虑其他因素),第二批每朵菊花的售价至少是多少元?
元(不考虑其他因素),第二批每朵菊花的售价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,其对称轴为直线
,其对称轴为直线![]() ,结合图象分析下列结论:①
,结合图象分析下列结论:①![]() ;②
;②![]() ;③当
;③当![]() 时,
时,![]() 随
随![]() 的增大而增大;④一元二次方程
的增大而增大;④一元二次方程![]() 的两根分别为
的两根分别为![]() ,
,![]() ;⑤
;⑤![]() ;⑥若
;⑥若![]() ,
,![]() 为方程
为方程![]() 的两个根,则
的两个根,则![]() 且
且![]() ,其中正确的结论有( )
,其中正确的结论有( )
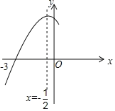
A. ![]() 个B.
个B. ![]() 个C.
个C. ![]() 个D.
个D. ![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】4件同型号的产品中,有1件不合格品和3件合格品.
(1)从这4件产品中随机抽取1件进行检测,求抽到的是不合格品的概率;
(2)从这4件产品中随机抽取2件进行检测,求抽到的都是合格品的概率;
(3)在这4件产品中加入x件合格品后,进行如下试验:随机抽取1件进行检测,然后放回,多次重复这个试验,通过大量重复试验后发现,抽到合格品的频率稳定在0.95,则可以推算出x的值大约是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】扫地机器人能够自主移动并作出反应,是因为它发射红外信号反射回接收器,机器人在打扫房间时,若碰到障碍物则发起警报.若某一房间内A、B两点之间有障碍物,现将A、B两点放置于平面直角坐标系xOy中(如图),已知点A,B的坐标分别为(0,4),(6,4),机器人沿抛物线y=ax2﹣4ax﹣5a运动.若机器人在运动过程中只触发一次报警,则a的取值范围是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,AB=AC=10cm,点D为△ABC内一点,∠BAD=15°,AD=6cm,连接BD,将△ABD绕点A逆时针方向旋转,使AB与AC重合,点D的对应点E,连接DE,DE交AC于点F,则CF的长为________cm.
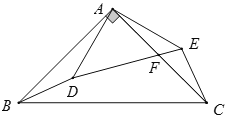
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“扬州漆器”名扬天下,某网店专门销售某种品牌的漆器笔筒,成本为30元/件,每天销售量![]() (件)与销售单价
(件)与销售单价![]() (元)之间存在一次函数关系,如图所示.
(元)之间存在一次函数关系,如图所示.

(1)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)如果规定每天漆器笔筒的销售量不低于240件,当销售单价为多少元时,每天获取的利润最大,最大利润是多少?
(3)该网店店主热心公益事业,决定从每天的销售利润中捐出150元给希望工程,为了保证捐款后每天剩余利润不低于3600元,试确定该漆器笔筒销售单价的范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com