练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】抛物线y＝ax2+bx﹣3与x轴交于A，B两点，与y轴交于点C，且OB＝OC＝3OA，求抛物线的解析式（　　）

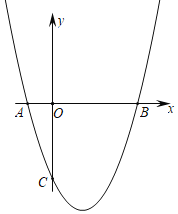
    A.y＝x2﹣2x﹣3B.y＝x2﹣2x+3C.y＝x2﹣2x﹣4D.y＝x2﹣2x﹣5

    【答案】A

    【解析】

    由抛物线与y轴的交点坐标可求OC得长，根据OB＝OC＝3OA，进而求出OB、OA，得出点A、B坐标，再用待定系数法求出函数的关系式.

    解：在抛物线y＝ax2+bx﹣3中，当x＝0时，y＝﹣3，点C（0，﹣3）

    ∴OC＝3，

    ∵OB＝OC＝3OA，

    ∴OB＝3，OA＝1，

    ∴A（﹣1，0），B（3，0）

    把A（﹣1，0），B（3，0）代入抛物线y＝ax2+bx﹣3得：

    a﹣b﹣3＝0，9a+3b﹣3＝0，

    解得：a＝1，b＝﹣2，

    ∴抛物线的解析式为y＝x2﹣2x﹣3，

    故选：A．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】解方程：

    （1）4（2x﹣1）2﹣36＝0；

    （2）x（x﹣3）+x﹣3＝0；

    （3）3x2﹣1＝4x；

    （4）（2x﹣3）2﹣5（2x﹣3）+6＝0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，三孔桥横截面的三个孔都呈抛物线形，两个小孔形状、大小都相同，正常水位时，大孔水面常度AB＝20米，顶点M距水面6米（即MO＝6米），小孔水面宽度BC＝6米，顶点N距水面4.5米．航管部门设定警戒水位为正常水位上方2米处借助于图中的平面直角坐标系解答下列问题：

    （1）在汛期期间的某天，水位正好达到警戒水位，有一艘顶部高出水面3米，顶部宽4米的巡逻船要路过此处，请问该巡逻船能否安全通过大孔？并说明理由．

    （2）在问题（1）中，同时桥对面又有一艘小船准备从小孔迎面通过，小船的船顶高出水面1.5米，顶部宽3米，请问小船能否安全通过小孔？并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】春季是传染病多发的季节，积极预防传染病是学校高度重视的一项工作，为此，某校对学生宿舍采取喷洒药物进行消毒.在对某宿舍进行消毒的过程中，先经过的集中药物喷洒，再封闭宿舍，然后打开门窗进行通风，室内每立方米空气中含药量与药物在空气中的持续时间之间的函数关系，在打开门窗通风前分别满足两个一次函数，在通风后又成反比例，如图所示.下面四个选项中错误的是（ ）

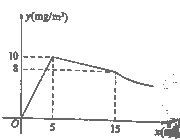
    A. 经过集中喷洒药物，室内空气中的含药量最高达到

    B. 室内空气中的含药量不低于的持续时间达到了

    C. 当室内空气中的含药量不低于且持续时间不低于35分钟，才能有效杀灭某种传染病毒.此次消毒完全有效

    D. 当室内空气中的含药量低于时，对人体才是安全的，所以从室内空气中的含药量达到开始，需经过后，学生才能进入室内

    查看答案和解析>>

    科目：初中数学 来源： 题型：

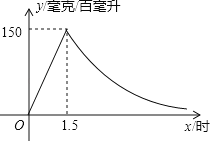
    【题目】实验数据显示，一般成人喝半斤低度白酒后，1.5小时内其血液中酒精含量y（毫克/百毫升）与时间x（时）成正比例；1.5小时后（包括1.5小时）y与x成反比例．根据图中提供的信息，解答下列问题：

    （1）写出一般成人喝半斤低度白酒后，y与x之间的函数关系式及相应的自变量取值范围；

    （2）按国家规定，车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升时属于“酒后驾驶”，不能驾车上路．参照上述数学模型，假设某驾驶员晚上21：00在家喝完半斤低度白酒，第二天早上7：00能否驾车去上班？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】综合与探究

    如图1，抛物线与轴交于，两点，与轴交于点．

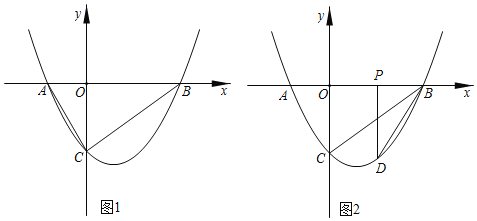
    （1）求抛物线的表达式；

    （2）点是抛物线上异于点的动点，若的面积与的面积相等，求出点的坐标；

    （3）如图2，当为的中点时，过点作轴，交抛物线于点.连接，将沿轴向左平移个单位长度（），将平移过程中与重叠部分的面积记为，求与的函数关系式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】随州市新水一桥（如图1）设计灵感来源于市花﹣﹣兰花，采用蝴蝶兰斜拉桥方案，设计长度为258米，宽32米，为双向六车道，2018年4月3日通车．斜拉桥又称斜张桥，主要由索塔、主梁、斜拉索组成．某座斜拉桥的部分截面图如图2所示，索塔AB和斜拉索（图中只画出最短的斜拉索DE和最长的斜拉索AC）均在同一水平面内，BC在水平桥面上．已知∠ABC=∠DEB=45°，∠ACB=30°，BE=6米，AB=5BD．

    （1）求最短的斜拉索DE的长；

    （2）求最长的斜拉索AC的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在初中阶段的函数学习中，我们经历了“确定函数的表达式﹣利用函数图象研究其性质﹣应用函数解决问题”的学习过程．在画函数图象时，我们通过描点或平移的方法画出了一个陌生函数的大致图象，结合上面经历的学习过程，现在来解决下面问题：在函数y＝中，当x＝0时，y＝1；当x＝2时，y＝．

    （1）求这函数的表达式　 　；

    （2）在给出的平面直角坐标系中画出这个函数的大致图象并写出这个函数的一条性质　 　；

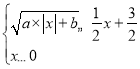    （3）结合你所画的函数图象与y＝x+的图象，直接写出不等式组的解集．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中有，为原点，，，将此三角形绕点顺时针旋转得到，抛物线过三点．

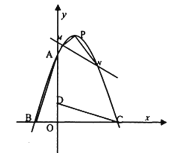
    （1）求此抛物线的解析式及顶点的坐标；

    （2）直线与抛物线交于两点，若，求的值；

    （3）抛物线的对称轴上是否存在一点使得为直角三角形．

    查看答案和解析>>

    同步练习册答案