
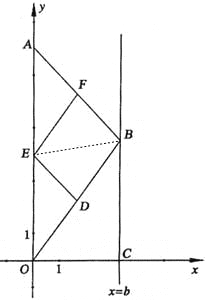
【题目】如图,在直角坐标系中,点A的坐标为(0,8),点 B(b,t)在直线x=b上运动,点D、E、F分别为OB、0A、AB的中点,其中b是大于零的常数.

(1)判断四边形DEFB的形状.并证明你的结论;
(2)试求四边形DEFB的面积S与b的关系式;
(3)设直线x=b与x轴交于点C,问:四边形DEFB能不能是矩形?若能.求出t的值;若不能,说明理由.
【答案】(1)平行四边形,证明见解析;(2)S=2b(b>0);(3)当0<b≤4时,四边形DEFB是矩形,这时,t=4±![]() ,当b>4时,四边形DEFB不是矩形.
,当b>4时,四边形DEFB不是矩形.
【解析】
解:(1)四边形DEFB是平行四边形.
证明:∵D、E分别是OB、OA的中点,
∴DE∥AB,同理,EF∥OB,
∴四边形DEFB是平行四边形;
(2)如图,连接BE,
S△AOB=![]() ×8×b=4b,
×8×b=4b,
∵E、F分别为OA、AB的中点,
∴S△AEF=![]() S△AEB=
S△AEB=![]() S△AOB=b,
S△AOB=b,
同理S△EOD=b,
∴S=S△AOB-S△AEF-S△ODE=4b-b-b=2b,
即S=2b(b>0);
(3)解法一:以E为圆心,OA长为直径的圆记为⊙E,
①当直线x=b与⊙E相切或相交时,若点B是切点或交点,则∠ABO=90°,由(1)知,四边形DEFB是矩形,
此时0<b≤4,可得△AOB∽△OBC,
∴![]()
![]()
,即OB2=OABC=8t,
在Rt△OBC中,OB2=BC2+OC2=t2+b2,
∴t2+b2=8t,
∴t2-8t+b2=0,
解得t=4±![]() ,
,
②当直线x=b与⊙E相离时,∠ABO≠90°,
∴四边形DEFB不是矩形,
综上所述:当0<b≤4时,四边形DEFB是矩形,这时,t=4±![]() ,当b>4时,四边形DEFB不是矩形;
,当b>4时,四边形DEFB不是矩形;
解法二:由(1)知,当∠ABO=90°时,四边形DEFB是矩形,
此时,Rt△OCB∽Rt△ABO,
∴![]() ,即OB2=OABC,
,即OB2=OABC,
又OB2=BC2+OC2=t2+b2,OA=8,BC=t(t>0),
∴t2+b2=8t,
∴(t-4)2=16-b2,
①当16-b2≥0时,解得t=4±![]() ,此时四边形DEFB是矩形,
,此时四边形DEFB是矩形,
②当16-b2<0时,t无实数解,此时四边形DEFB不是矩形,
综上所述:当16-b2≥0时,四边形DEFB是矩形,此时t=4±![]() ,当16-b2<0时,四边形DEFB不是矩形;
,当16-b2<0时,四边形DEFB不是矩形;
解法三:如图,过点A作AM⊥BC,垂足为M,

在Rt△AMB中,AB2=AM2+BM2=b2+(8-t)2,
在Rt△OCB中,OB2=OC2+BC2=b2+t2,
在Rt△OAB中,当AB2+OB2=OA2时,∠ABO=90°,则四边形DEFB为矩形,
∴b2+(8-t)2+b2+t2=82,
化简得t2-8t=-b2,配方得(t-4)2=16-b2,其余同解法二.


科目:初中数学 来源: 题型:
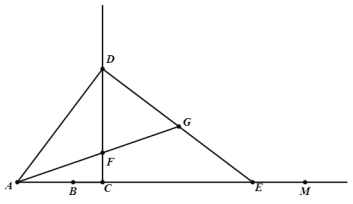
【题目】如图,射线AM上有一点B,AB=6.点C是射线AM上异于B的一点,过C作CD⊥AM,且CD=![]() AC.过D点作DE⊥AD,交射线AM于E. 在射线CD取点F,使得CF=CB,连接AF并延长,交DE于点G.设AC=3x.
AC.过D点作DE⊥AD,交射线AM于E. 在射线CD取点F,使得CF=CB,连接AF并延长,交DE于点G.设AC=3x.
(1) 当C在B点右侧时,求AD、DF的长.(用关于x的代数式表示)
(2)当x为何值时,△AFD是等腰三角形.
(3)若将△DFG沿FG翻折,恰使点D对应点![]() 落在射线AM上,连接
落在射线AM上,连接![]() ,
,![]() .此时x的值为 (直接写出答案)
.此时x的值为 (直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购进![]() 、
、![]() 两种商品,购买1个
两种商品,购买1个![]() 商品比购买1个
商品比购买1个![]() 商品多花10元,并且花费300元购买
商品多花10元,并且花费300元购买![]() 商品和花费100元购买
商品和花费100元购买![]() 商品的数量相等.
商品的数量相等.
(1)求购买一个![]() 商品和一个
商品和一个![]() 商品各需要多少元;
商品各需要多少元;
(2)商店准备购买![]() 、
、![]() 两种商品共80个,若
两种商品共80个,若![]() 商品的数量不少于
商品的数量不少于![]() 商品数量的4倍,并且购买
商品数量的4倍,并且购买![]() 、
、![]() 商品的总费用不低于1000元且不高于1050元,那么商店有哪几种购买方案?
商品的总费用不低于1000元且不高于1050元,那么商店有哪几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点![]() 坐标为
坐标为![]() 轴上点
轴上点![]() ,将线段
,将线段![]() 绕着点
绕着点![]() 顺时针旋转
顺时针旋转![]() 得到
得到![]() ,过点
,过点![]() 作直线
作直线![]() 轴于
轴于![]() ,过点
,过点![]() 作
作![]() 直线
直线![]() 于
于![]() .
.
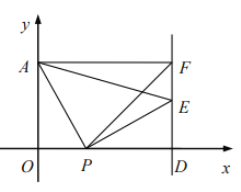
(1)当点![]() 是
是![]() 的中点时,求直线
的中点时,求直线![]() 的函数表达式.
的函数表达式.
(2)当![]() 时,求
时,求![]() 的面积.
的面积.
(3)在直线![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ?若存在,试用
?若存在,试用![]() 的代数式表示点
的代数式表示点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①所示,已知正方形ABCD和正方形AEFG,连接DG,BE.
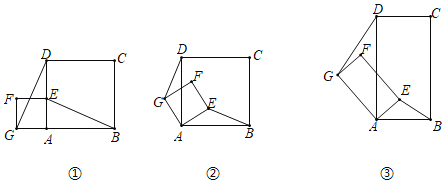
(1)发现:当正方形AEFG绕点A旋转,如图②所示.
①线段DG与BE之间的数量关系是 ;
②直线DG与直线BE之间的位置关系是 ;
(2)探究:如图③所示,若四边形ABCD与四边形AEFG都为矩形,且AD=2AB,AG=2AE时,上述结论是否成立,并说明理由.
(3)应用:在(2)的情况下,连接BG、DE,若AE=1,AB=2,求BG2+DE2的值(直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将如图所示的牌面数字1、2、3、4的四张扑克牌背面朝上,洗匀后放在桌面上.

(1)从中随机抽出一张牌,牌面数字是奇数的概率是 ;
(2)从中随机抽出两张牌,两张牌牌面数字的和是6的概率是 ;
(3)先从中随机抽出一张牌,将牌面数字作为十位上的数字,然后将该牌放回并重新洗匀,再随机抽取一张,将牌面数字作为个位上的数字,请用树状图或列表的方法求组成的两位数恰好是3的倍的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家医保局相关负责人3月25日表示,2019年底前我国将实现生育保险基金并入职工基本医疗保险基金,统一征缴,就是通常所说的“五险变四险”.传统的五险包括:养老保险、失业保险、医疗保险、工伤保险、生育保险.某单位从这五险中随机抽取两种,为员工提高保险比例,则正好抽中养老保险和医疗保险的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
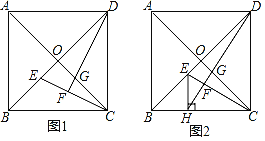
【题目】已知正方形ABCD的对角线AC,BD相交于点O.
(1)如图1,E,G分别是OB,OC上的点,CE与DG的延长线相交于点F.若DF⊥CE,求证:OE=OG;
(2)如图2,H是BC上的点,过点H作EH⊥BC,交线段OB于点E,连结DH交CE于点F,交OC于点G.若OE=OG,
①求证:∠ODG=∠OCE;
②当AB=1时,求HC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知图形![]() 和图形
和图形![]() 上的两点
上的两点![]() 、
、![]() ,如果
,如果![]() 上的所有点都在图形
上的所有点都在图形![]() 的内部或边上,则称
的内部或边上,则称![]() 为图形
为图形![]() 的内弧.特别的,在
的内弧.特别的,在![]() 中,
中,![]() ,
,![]() 分别是
分别是![]() 两边的中点,如果
两边的中点,如果![]() 上的所有点都在
上的所有点都在![]() 的内部或边上,则称
的内部或边上,则称![]() 为
为![]() 的中内弧.(注:
的中内弧.(注:![]() 是指劣弧或半圆)在平面直角坐标系中,已知点
是指劣弧或半圆)在平面直角坐标系中,已知点![]()
![]() .设内弧所在圆的圆心为
.设内弧所在圆的圆心为![]() .
.
(1)当![]() 时,连接
时,连接![]() 、
、![]() 并延长.
并延长.
①请在图1中画出一条![]() 的内弧
的内弧![]() ;
;
②请直接写出![]() 的内弧
的内弧![]() 长度的最大值__________.
长度的最大值__________.
(2)连接![]() 、
、![]() 并延长.
并延长.
①当![]() 时,请直接写出
时,请直接写出![]() 的所有内弧
的所有内弧![]() 所在圆的圆心
所在圆的圆心![]() 的纵坐标的取值范围__________;
的纵坐标的取值范围__________;
②若直线![]() 上存在
上存在![]() 的内弧
的内弧![]() 所在圆的圆心
所在圆的圆心![]() ,请求出
,请求出![]() 的取值范围.
的取值范围.
(3)作点![]() 关于点
关于点![]() 的对称点
的对称点![]() ,作点
,作点![]() 关于点
关于点![]() 的对称点
的对称点![]() ,连接
,连接![]() 、
、![]() 、
、![]() .令
.令![]() ,当
,当![]() 的中内弧
的中内弧![]() 所在的圆的圆心
所在的圆的圆心![]() 在
在![]() 的外部时,
的外部时,![]() 的所有中内弧
的所有中内弧![]() 都存在,请直接写出
都存在,请直接写出![]() 的取值范围__________.
的取值范围__________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com